Graphe (Bac 🎯)⚓︎
Définition⚓︎
Point de cours 1 : définition d'un graphe
Un graphe est un ensemble d'objets appelés sommets dont certains reliés deux à deux par des liaisons appelées arcs.
En général on associe une étiquette ou nom à chaque sommet.
Il existe deux grandes familles de graphes :
- si les arcs peuvent être orientés on parle de graphe orienté
- sinon de graphe non orienté.
On peut aussi associer une étiquette, en général une valeur numérique appelée poids, à chaque arc : dans ce cas on parle de graphe pondéré (qui peut être orienté ou non).
Conventions de représentation graphique :
| Type de graphe | Sommet | Arc |
|---|---|---|
| Non orienté | Disque avec étiquette | i - jreprésenté par un segment |
| Orienté | Disque avec étiquette | i -> jreprésenté par une flèche orientée |
Exemple de graphe non orienté⚓︎
Exemple de graphe non orienté pondéré"⚓︎
Exemple de graphe orienté⚓︎
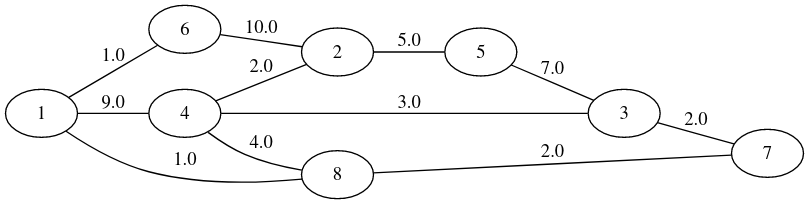
Exemple de graphe orienté pondéré"⚓︎
Vocabulaire des graphes⚓︎
Point de cours 2 : vocabulaire des graphes
Sauf mention explicite, les définitions suivantes sont valables pour les graphes orientés ou non orientés. Dans les exemples, pour simplifier on assimile un sommet à son étiquette (qui ici est un entier).
Un graphe est un ensemble de sommets et d'arcs⚓︎
Un graphe est défini par un ensemble V de sommets (vertices en anglais) et un ensemble E d'arcs (edges en anglais) qui sont des couples de sommets.
Les arcs peuvent être orientés ou non orientés.
Un arc est une relation d'adjacence entre deux sommets⚓︎
Si un arc a pour origine le sommet \(x\) et pour extrémité le sommet \(y\), on dit que :
- \(y\) est adjacent à \(x\) ou que \(y\) est un voisin de \(x\).
- \(y\) est un successeur de \(x\) et que \(x\) est un prédécesseur de \(y\)
Pour un arc non orienté, on ne distingue pas prédécesseur et successeur et la relation d'adjacence est symétrique : si \(y\) est voisin de \(x\) alors \(x\) est voisin de \(y\).
On note \(x\) -> \(y\) un arc orienté et \(x - y\) un arc non orienté. Pour un arc orienté, on distingue l'arc \(x\) -> \(y\) de l'arc \(y\) -> \(x\).
Exemples
Adjacence dans un graphe non orienté⚓︎
Le sommet 2 est adjacent aux sommets 1, 3 et 4 : il a trois voisins.
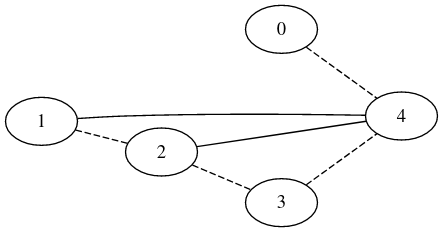
Adjacence dans un graphe orienté⚓︎
Le sommet 2 a deux voisins 3 et 4.
Le sommet 2 est un voisin du sommet 1 mais la réciproque est fausse : l'arc orienté 1 -> 2 définit 1 comme prédécesseur de 2 et 2 comme successeur de 1.
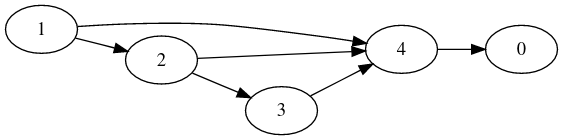
Un chemin est une séquence d'arcs consécutifs⚓︎
Un chemin est une séquence d'arcs consécutifs :
Ainsi le chemin \(x_{0}\) -> \(x_{1}\) -> \(x_{2}\) ... -> \(x_{n}\) part de l'origine \(x_{0}\) puis par le sommet \(x_{1}\), puis le sommet \(x_{2}\) et conduit jusqu'à l'extrémité \(x_{n}\) en suivant des arcs consécutifs.
La longueur d'un chemin est le nombre d'arcs qui le constitue.
Un chemin simple est un chemin sans répétition d'arcs.
Un cycle est un chemin dont l'extrémité coincide avec l'origine.
Exemples
Chemin dans un graphe non orienté⚓︎
0 - 4 - 3 - 2 - 1 est un chemin de longueur 4 dans le graphe non orienté ci-dessous.
4 - 3 - 2 - 4 est un cycle de longueur 3 dans ce même graphe.

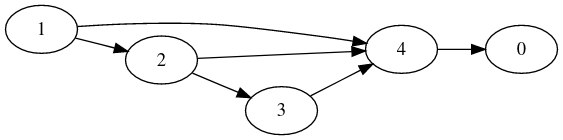
Chemin dans un graphe orienté⚓︎
1 -> 2 -> 3 -> 4 - > 0 est un chemin de longueur 4 dans le graphe orienté ci-dessous.
Ce graphe orienté ne contient pas de cycles.

Degré d'un arc⚓︎
Dans un graphe orienté :
- le degré sortant d'un sommet est le nombre d'arcs dont ce sommet est l'origine : c'est le nombre de successeurs de ce sommet
- le degré entrant d'un sommet est le nombre d'arcs dont ce sommet est l'extrémité : c'est le nombre de prédécesseurs de ce sommet
Dans un graphe non orienté, on ne distingue pas degré sortant et degré entrant : le degré d'un sommet est le nombre d'arcs dont il est une extrémité, c'est le nombre de voisins du sommet.
Interface⚓︎
Point de cours 3 : une interface pour une classe Graphe
Pour implémenter les algorithmes de graphe auy programme, l'interface minimale ci-dessous sera suffisante. Le choix d'une structure de données de représentation du graphe dépend de l'implémentation choisie et sera développé dans la section suivante.
L'interface est donnée pour un graphe non orienté et implémentée avec une représentation par dictionnaire d'adjacences (voir section suivante).
class Graphe:
def __init__(self, liste_sommets):
"""
Crée une représentation de graphe non orienté à partir d'une liste de sommets
"""
self.liste_sommets = liste_sommets
self.adjacents = {sommet : [] for sommet in liste_sommets}
def sommets(self):
"""
Renvoie une liste des sommets
"""
return self.liste_sommets
def ajoute_arc(self, sommetA, sommetB):
"""
Ajoute dans la représentation de graphe l'arc sommetA - sommetB
"""
assert (sommetA in self.liste_sommets), "sommet A pas dans le graphe"
assert (sommetB in self.liste_sommets), "sommet B pas dans le graphe"
self.adjacents[sommetA].append(sommetB)
# ligne suivante uniquement pour graphe non orienté
self.adjacents[sommetB].append(sommetA)
def voisins(self, sommet):
"""
Renvoie une liste des voisins du sommet dans la représentation du graphe
"""
assert sommet in self.liste_sommets, "sommet pas dans le graphe"
return self.adjacents[sommet]
def est_arc(self, sommetA, sommetB):
"""
Renvoie un booléen indiquant si l'arc sommetA - sommetB appartient au graphe
"""
assert sommetA in self.liste_sommets, "sommetA pas dans le graphe"
return sommetB in self.adjacents[sommetA]
Différentes représentations d'un graphe⚓︎
Représentation par matrice d'adjacence⚓︎
Point de cours 4 : représentation par matrice d'adjacence
- On étiquette les sommets de 0 à \(n-1\).
- On représente chaque arc dans une matrice d'adjacence, c'est-à-dire un tableau à deux dimensions où on inscrit un 1 en ligne
iet colonnejsi l'arci -> jest dans le graphe.
Matrice d'adjacence en Python
En Python, on peut représenter une matrice d'adjacences d'un graphe à \(n\) sommets par une liste de \(n\) listes de taille \(n\). Si cette matrice est référencée par une variable mat et si 0 <= i < n et 0 <= j < n alors :
mat[i][j]vaut 1 si l'arci -> jest dans le graphemat[i][j]vaut 0 si l'arci -> jn'est pas dans le graphe
💡 Pour un graphe non orienté, on ne distingue pas les arcs
i -> jetj -> idonc s'il y a un 1 en ligneiet colonnejalors il y a un 1 en lignejet colonnei. On dit que la matrice d'adjacence est symétrique.💡 Pour un graphe pondéré on peut remplacer le 1 marquant la présence d'un arc par le poids de l'arc.
Exemple avec un graphe non orienté
Source : exemple de Cédric Gouygou
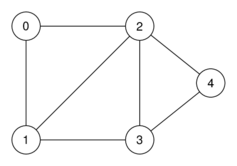
Le graphe non orienté ci-dessus peut être représenté par la matrice d'adjacence ci-dessous. La matrice est symétrique.

Voici une représentation en Python :
[[0, 1, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 1, 0, 1, 1],
[0, 1, 1, 0, 1],
[0, 0, 1, 1, 0]
]
Représentation par tableau de listes d'adjacence⚓︎
Point de cours 5 : représentation par tableau de listes d'adjacence
- On étiquette les sommets de 0 à \(n-1\).
- On crée un tableau de taille \(n\) dont l'élément d'indice
icontient la liste des sommetsjadjacents au sommeti, c'est-à-dire tels que l'arci -> jexiste. Cette liste d'adjacence du sommeticontient donc :- tous les voisins de
idans un graphe non orienté - tous les successeurs de
idans un graphe orienté
- tous les voisins de
Listes d'adjacence en Python
En Python, on peut représenter un tableau de listes d'adjacences par une liste de \(n\) listes de tailles variables (contrairement à une matrice d'adjacence où toutes les listes sont de taille \(n\)). Si cette liste est référencée par une variable adj et si 0 <= i < n et 0 <= j < n alors :
len(adj)vaut \(n\) car le graphe a \(n\) sommetsadj[i]contient la liste de tous les sommetsjtels que l'arci -> jexistelen(adj[i])est donc le nombre de voisins (graphe non orienté) ou successeurs (graphe orienté) du sommeti
Exemple avec un graphe non orienté
Source : exemple de Cédric Gouygou

Le graphe non orienté ci-dessus peut être représenté en Python par listes d'adjacences comme ci-dessous.
adj = [[1, 2],
[0, 2, 3],
[0, 1, 3, 4],
[1, 2, 4],
[2, 3]
]
La valeur de adj[0] est la liste [1, 2] car les voisins du sommet 0 sont les sommets 1 et 2.
Il faut noter que par symétrie, comme le graphe est non orienté, 0 appartient aux listes d'adjacence adj[1] et à adj[2].
Représentation par dictionnaire de listes d'adjacence⚓︎
Point de cours 6 : représentation par dictionnaire de listes d'adjacence
On considère un graphe de \(n\) sommets étiquetés par des noms (type 'str'). On peut reprendre le modèle de représentation par un tableau de listes d'adjacences en remplaçant le tableau par un dictionnaire dont les clefs sont les étiquettes des sommets.
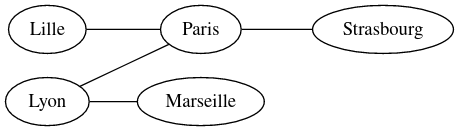
Voici un exemple de graphe avec sommets étiquetés, représenté par un dictionnaire de listes d'adjacences en Python.

adj_tgv = {"Lyon": ["Paris", "Marseille"],
"Lille": ["Paris"],
"Marseille": ["Lyon"],
"Paris": ["Lille", "Lyon", "Strasbourg"],
"Strasbourg": ["Paris"]}
Comparaison des représentations⚓︎
Comparaison des représentations
Complexité spatiale⚓︎
Soit un graphe avec un ensemble V de sommets et un ensemble E d'arcs.
Notons \(n\) =|V| le nombre de sommets et \(m\)= |E| le nombre d'arcs.
| Représentation | Complexité spatiale |
|---|---|
| Matrice d'adjacence | quadratique par rapport au nombre de sommets \(O(n^{2})\) |
| Listes d'adjacence | \(O(n+m)\) |
On rappelle l'inégalité \(n - 1 \leqslant m < n^{2}\).
À l'exception des graphes denses dont le nombre d'arcs est de complexité quadratique par rapport au nombre de sommets, la complexité spatiale d'un tableau de listes d'adjacences est bien meilleure que celle d'une matrice d'adjacence.
Complexité temporelle⚓︎
Les deux opérations de base sur une représentation de graphe sont :
- le test d'adjacence : l'arc
i->jexiste-t-il ? - la liste des voisins (graphe non orienté) ou successeurs (graphe orienté)
Ces opérations ont une complexité par rapport au nombre de sommets \(n\), différente selon les représentations. On donne juste la complexité dans le pire des cas.
| Représentation | Tester si l'arc i->j existe |
Complexité |
|---|---|---|
| Matrice d'adjacence | mat[i][j] == 1 |
constante \(O(1)\) |
| Listes d'adjacence | j in adj[i] |
linéaire \(O(n)\) |
| Représentation | Lister les voisins/successeurs | Complexité |
|---|---|---|
| Matrice d'adjacence | [j for j in range(n) if mat[i][j] == 1] |
linéaire \(O(n)\) |
| Listes d'adjacence | adj[i] |
constante \(O(1)\) |
En pratique, les algorithmes de parcours de graphe au programme utilisent surtout l'opération de liste des voisins/successeurs, donc les listes d'adjacences seront la représentation privilégiée.
💡 Les performances d'un dictionnaire de listes d'adjacences sont comparables à celles d'un tableau de listes d'adjacences. Il serait possible d'améliorer le test d'existence d'un arc, de linéaire à constant, si on utilisait une table de hachage à la place d'une liste d'adjacences, par exemple un ensemble de type
seten Python.