Tri fusion (Bac 🎯)

Ce cours est mis à disposition selon les termes de la Licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.

Sources et crédits pour ce cours

Pour préparer ce cours, j'ai utilisé :

• le manuel NSI chez Ellipses de Balabonski, Conchon, Filliâtre, Nguyen
• le cours de mon collègue Pierre Duclosson
• la ressource Eduscol sur la méthode Diviser pour régner.
• le module trifusionviz de David Cobac pour générer des arbres d'appels du tri fusion.

🔖 Synthèse de ce qu'il faut retenir pour le bac

Un algorithme de tri Diviser pour Régner

Exercice 4

Question 1

On a représenté par le schéma ci-dessous, la trace d'exécution d'un algorithme qui trie dans l'ordre croissant le tableau d'entiers [6, 3, 5, 2, 4, 0, 7 , 1] avec une méthode Diviser pour Régner.

énoncésolution

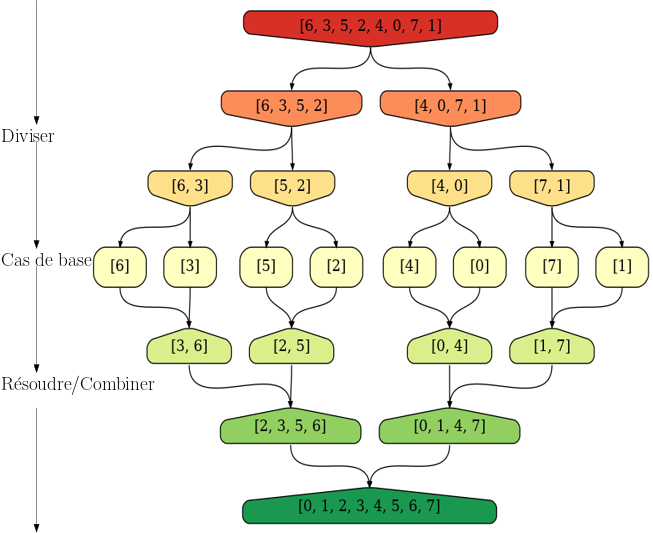
Recopiez puis complétez ce nouveau schéma pour trier le tableau d'entiers [6, 3, 5, 2, 4, 0, 7 , 1] avec le même algorithme.

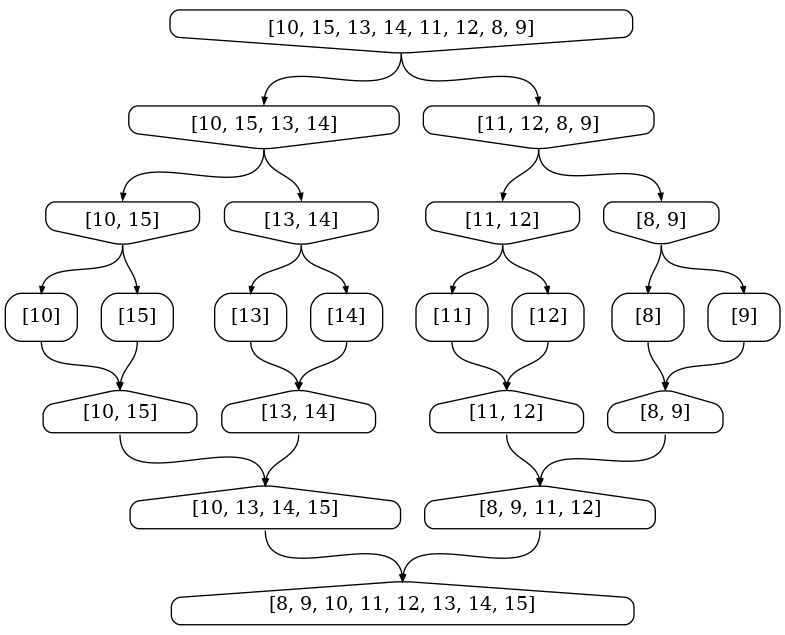
Question 2

énoncésolution

Dessinez un nouveau schéma pour trier le tableau d'entiers [11, 10, 12, 8, 9] avec le même algorithme.

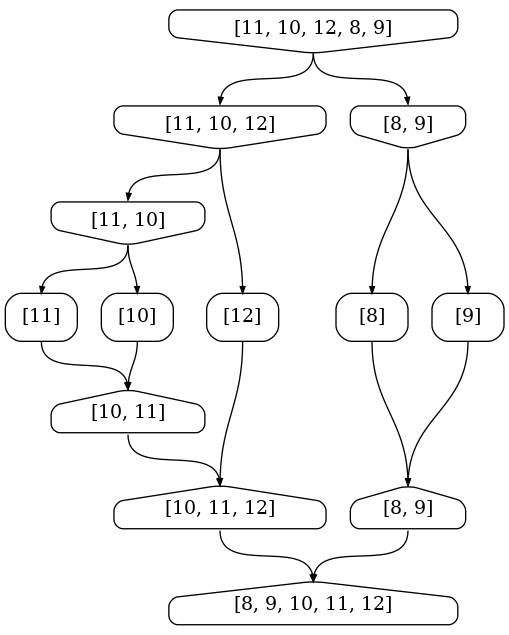
Question 3

On suppose qu'on dispose d'une fonction fusion qui prend en paramètres deux tableaux d'entiers t1 et t2 triés dans l'ordre croissant et qui renvoie le tableau trié dans l'ordre croissant, qui est constitué de la réunion les éléments de t1 et t2.

🐍 Script Python

>>> t1 = [6, -3, 6, 7]
>>> t2 = [8, -4, 6]
>>> fusion(t1, t2)
[-4, -3, 6, 6, 6, 7, 8]

énoncésolution

Complétez la fonction tri_fusion pour qu'elle implémente cet algorithme de tri.

Découpage en tranche

On peut extraire d'un tableau Python t des sous-tableaux avec un découpage en tranches. Les délimitations des tranches fonctionnent comme pour range, borne incluse à gauche et exclue à droite.

• t[a:b] : sous-tableau avec tous les éléments d'indice i tels que a <= i < b
• t[:b] : sous-tableau avec tous les éléments d'indice i tels que 0 <= i < b
• t[a:] : sous-tableau avec tous les éléments d'indice i tels que a <= i < len(t)

L'absence de borne représente l'indice minimal à gauche ou maximal à droite.

🐍 Script Python

def tri_fusion(t):
    """Renvoie un tabbleau avec les mêmes éléments que t tableau d'entiers
    mais dans l'ordre croissant"""
    # cas de base:
    if len(t) <= 1:
        ...
    # diviser
    m = len(t) // 2
    # résoudre les sous-problèmes
    t1 = ...
    ...
    # combiner
    t3 = ...
    return t3

🐍 Script Python

def tri_fusion(t):
    """Renvoie un tabbleau avec les mêmes éléments que t tableau d'entiers
    mais dans l'ordre croissant"""
    # cas de base:
    if len(t) <= 1:
        return t
    # diviser
    m = len(t) // 2
    # résoudre les sous-problèmes
    t1 = tri_fusion(t[:m])
    t2 = tri_fusion(t[m:])
    # combiner
    t3 = fusion(t1, t2)
    return t3

Point de cours 2

L'algorithme de tri par fusion permet de trier un tableau t d'éléments comparables avec une méthode Diviser pour Régner :

1. Diviser : on découpe le tableau en son milieu m et on se ramène à deux sous-problèmes similaires et plus petits :
   • trier le premier sous-tableau avec les éléments d'indice inférieur ou égal à m
   • trier le second sous-tableau avec les éléments d'indice supérieur à m
2. Résoudre : on résout les deux sous-problèmes en appelant récursivement l'algorithme sur chaque sous-tableau et on obtient deux sous-tableaux triés t1 et t2.
3. Combiner : on fusionne les deux sous-tableaux triés t1 et t2 en un tableau trié t3 contenant les mêmes éléments que t.

🐍 Script Python

def tri_fusion(t):
    """Renvoie un tableau avec les mêmes éléments que t tableau d'entiers
    mais dans l'ordre croissant"""
    # cas de base:
    if len(t) <= 1:
        return t
    # diviser
    m = len(t) // 2
    # résoudre les sous-problèmes
    t1 = tri_fusion(t[:m])
    t2 = tri_fusion(t[m:])
    # combiner
    t3 = fusion(t1, t2)
    return t3

Remarque

Cette version n'est pas optimale au niveau de la complexité en espace car elle renvoie un nouveau tableau lors de chaque appel. On donnera plus loin une version qui effectue un tri en place, utilisant un seul tableau de stockage temporaire. De plus on pourra aussi éviter le découpage en tranches qui en Python coûte cher : il faut recopier tous les éléments de la tranche.

La fonction de fusion

Exercice 5

Question 1

Pour fusionner deux tableaux d'éléments comparables triés dans l'ordre croissant, on crée un tableau vide t3 et on répète les étapes suivantes :

• étape 1 : si tous les éléments n'ont pas été sélectionnés dans t1 et dans t2 on passe à l'étape 2 sinon à l'étape 3
• étape 2 : on compare le plus petit élément non sélectionné de t1 avec le petit élément non sélectionné de t2 et on sélectionne le plus petit des deux pour le placer à la fin de t3, puis on revient à l'étape 1
• étape 3 : il reste des éléments non sélectionnés dans un seul des deux tableaux t1 ou t2, on sélectionne les éléments restants dans l'ordre croissant pour les placer à la fin de t3. L'algorithme est ensuite terminé.

énoncésolution

Appliquez cet algorithme pour fusionner les tableaux d'entiers triés t1 = [4, 8, 9, 9] et t2 = [5, 8, 10], dans un tableau d'avancement comme celui-ci :

sélectionnés dans t1	restants dans t1	sélectionnés dans t2	restants dans t2	t3
4	8, 9, 9		5, 8, 10	4
...	...	...	...	...

sélectionnés dans t1	restants dans t1	sélectionnés dans t2	restants dans t2	t3
4	8, 9, 9		5, 8, 10	4
4	8, 9, 9	5	8, 10	4, 5
4, 8	9, 9	5	8, 10	4, 5, 8
4, 8	9, 9	5, 8	10	4, 5, 8, 8
4, 8, 9	9	5, 8	10	4, 5, 8, 8, 9
4, 8, 9, 9		5, 8	10	4, 5, 8, 8, 9
4, 8, 9, 9		5, 8, 10		4, 5, 8, 8, 9, 10

Question 2

énoncésolution

💻 Saisir ses réponses sur Capytale

Complétez ci-dessous la fonction fusion qui prend en paramètres deux tableaux d'entiers triés dans l'ordre croissant et renvoie un tableau trié dans l'ordre croissant obtenu en réunissant les éléments de t1 et t2.

Les deux tableaux t1 et t2 ne doivent pas être modifiés.

###

Lancer Télécharger Téléverser Recharger Sauvegarder

def fusion(t1, t2):bksl-nl """bksl-nl Fusionne les tableaux d'entiers t1 et t2 triés dans l'ordre croissant en un tableau t3 trié dans l'ordre croissant et constitué des mêmes éléments que t1 et t2 bksl-nl """bksl-nl n1 = len(t1)bksl-nl n2 = len(t2)bksl-nl t3 = []bksl-nl i1, i2 = 0, 0bksl-nl while i1 < n1 and ...:bksl-nl # à compléterbksl-nl ...bksl-nl # ici un des deux tableaux t1 ou t2 est videbksl-nl # cas il reste t1 non videbksl-nl while i1 < n1:bksl-nl # à compléterbksl-nl ...bksl-nl # cas il reste t2 non videbksl-nl while i2 < n2:bksl-nl # à compléterbksl-nl ...bksl-nl return t3bksl-nlbksl-nldef testpy-undfusion():bksl-nl """bksl-nl Jeu de tests unitaires pour la fonction fusionbksl-nl de signature foncpy-undfusion(t1, t2)bksl-nl qui fusionne les tableaux t1 et t dans l'ordre croissantbksl-nl en un tableau t3 dans l'ordre croissantbksl-nl """bksl-nl assert fusion([1, 4], [3]) == [1, 3, 4]bksl-nl assert fusion([1, 4], []) == [1,4]bksl-nl assert fusion([1, 4], [0, 5]) == [0, 1, 4, 5]bksl-nl print("tests réussis")bksl-nl

🐍 Script Python

def fusion(t1, t2):
    """
    Fusionne les tableaux d'entiers  t1 et t2 triés dans l'ordre croissant en un tableau  t3 trié dans l'ordre croissant  et constitué des mêmes    éléments  que t1 et t2  
    """
    n1 = len(t1)
    n2 = len(t2)
    t3 = []
    i1, i2 = 0, 0
    while i1 < n1 and i2 < n2:
        if t1[i1] <= t2[i2]:
            t3.append(t1[i1])
            i1 = i1 + 1
        else:
            t3.append(t2[i2])
            i2 = i2 + 1
    # ici un des deux tableaux t1 ou t2 est vide
    # cas il reste t1 non vide
    while i1 < n1:
        t3.append(t1[i1])
        i1 = i1 + 1
    # cas il reste t2 non vide
    while i2 < n2:
        t3.append(t2[i2])
        i2 = i2 + 1
    return t3

Exercice 6

On rappelle la fonction de fusion établie dans l'exercice précédent.

fonction de fusion

La version la plus simple à coder.

🐍 Script Python

def fusion(t1, t2):
    n1 = len(t1)
    n2 = len(t2)
    t3 = []
    i1, i2 = 0, 0
    while i1 < n1 and i2 < n2:
        if t1[i1] <= t2[i2]:
            t3.append(t1[i1])
            i1 = i1 + 1
        else:
            t3.append(t2[i2])
            i2 = i2 + 1
    while i1 < n1:
        t3.append(t1[i1])
        i1 = i1 + 1
    while i2 < n2:
        t3.append(t2[i2])
        i2 = i2 + 1
    return t3

Une autre version plus pratique pour démontrer la correction.

🐍 Script Python

def fusion(t1, t2):
    n1 = len(t1)
    n2 = len(t2)
    t3 = []
    i1, i2 = 0, 0
    while i1 + i2 < n1 + n2:
        if (i1 < n1 and i2 < n2 and t1[i1] <= t2[i2]) or (i1 < n1 and i2 == n2):
            t3.append(t1[i1])
            i1 = i1 + 1
        else:
            t3.append(t2[i2])
            i2 = i2 + 1
    return t3

Question 1 : terminaison de la fonction fusion

énoncésolution

Démontrez que n1 + n2 - (i1 + i2) est un variant pour la boucle while de la seconde version de la fonction fusion donnée ci-dessus. On peut alors en déduire que cette boucle se termine.

• (P1) n1 + n2 - (i1 + i2) est un entier avant l'entrée dans la boucle puisque sa valeur est alors n1 + n2
• (P2) La boucle s'exécute ssi i1 + i2 < n1 + n2, donc pour une valeur de n1 + n2 - (i1 + i2) supérieure à zéro
• (P3) : Si on suppose qu'une itération de boucle s'exécute avec n1 + n2 - (i1 + i2) entier positif en entrée de boucle, en sortie de boucle i1 ou i2 a été incrémenté de 1 et donc n1 + n2 - (i1 + i2) est un entier de valeur strictement inférieure à sa valeur en entrée de boucle.

Les propriétés (P1), (P2) et (P3) étant vérifiées, on en déduit que n1 + n2 - (i1 + i2) est un variant de la première boucle while, qui donc se termine.

Question 3 : correction de la fonction fusion

énoncésolution

On note :

• j le nombre d'éléments sélectionnés dans le tableau fusionné t3
• i1 l'indice du premier élément non sélectionné dans t1
• i2 l'indice du premier élément non sélectionné dans t2

On définit la propriété (P) suivante :

Les j premiers éléments de t3 sont triés et t3[j - 1] est inférieur ou égal à t1[i1] et t2[i2]

Démontrez que (P) est un invariant de la première boucle while.

On admet que c'est aussi un invariant des deux boucles suivantes.

Concluez sur la correction de la fonction fusion.

• Initalisation : Avant la première boucle j vaut 0 donc la propriété (P) est vraie

• Préservation : Supposons que la propriété (P) soit vraie avant une itération de boucle qui s'exécute.

  • Cas où t1[i1] <= t2[i2]. En début de boucle, t3 est trié et son plus grand élément t3[j-1] est inférieur ou égal à t1[i1] donc en ajoutant t1[i1] à la fin de t3, on garde t3 dans l'ordre croissant. On incrémente j. On a alors t3[j]=t1[i1] <= t2[i2]. De plus t1 dans l'ordre croissant donc t3[j] = t1[i1] <= t1[i1+1]. Si on incrémente i1, on a bien encore t3[j] <= t1[i1+1]. Ainsi la propriété (P) est encore vraie en sortie de boucle.
  • Le cas où t1[i1] > t2[i2] est symétrique.

On en déduit que (P) est un invariant de la première boucle while.On peut démontrer de façon similaire que c'est aussi un invariant des deux boucles suivantes. On peut alors conclure que (P) est vraie à la fin de la fonction fusion dont on a déjà prouvé la terminaison. A cette étape, on a i1 = n1 et i2 = n2 et j = n1 + n2 donc le tableau t3 est complet et il est trié par propriété de l'invariant. Il contient exactement les éléments de t1 plus les éléments de t2.

Question 3 : complexité de la fonction fusion

énoncésolution

Quel est le nombre total de comparaisons et d'ajouts d'éléments à la fin de t3 effectuées par la fonction fusion ?

En déduire la complexité de la fonction fusion en fonction des tailles des tableaux fusionnés t1 et t2.

Chaque itération d'une des trois boucles while, se traduit par une comparaison, une itération de i1 ou i2 et un ajout dans t3. L'algorithme se termine après n1 + n2 itérations de l'une des trois boucles, autant de comparaisons et d'ajouts dans t3. La complexité de la fonction fusion est donc en \(O(n1+n2)\).

Analyse du tri fusion

Exercice 6

On admet la terminaison, la correction et la complexité de la fonction ̀fusion établies dans l'exercice 5.

Question 1 : terminaison

énoncésolution

Justifier que l'algorithme de tri _fusion se termine, à l'aide d'un raisonnement par récurrence.

La fonction tri_fusion est récursive donc elle se termine si les appels récursifs convergent vers un cas de base.

On peut le démontrer à l'aide d'un raisonnement par récurrence forte. On note \(n \geqslant 0\) la taille du tableau.

• Initialisation : Si \(n \leqslant 1\), alors la fonction renvoie le tableau et se termine quel que soit le tableau.
• Hérédité : On appelle la fonction sur un tableau de taille \(n>1\). On suppose que la fonction se termine pour tous les tableaux de taille \(<n\).
  • Les deux appels récursifs de l'étape Résoudre sont effectués sur des sous-tableaux de taille \(\leqslant n/2\) donc se terminent par hypothèse de récurrence forte.
  • L'appel de la fonction fusion se termine d'après l'exercice 5
  • On en déduit que l'appel de la fonction tri_fusion sur le tableau de taille \(n\) se termine.

Par récurrence forte, on en déduit que la fonction se termine pour tous les tableaux de taille \(n \geqslant 0\).

Question 2 : correction du tri fusion

énoncésolution

Justifier que l'algorithme de tri _fusion est correct, à l'aide d'un raisonnement par récurrence.

On peut le démontrer à l'aide d'un raisonnement par récurrence forte. On note \(n \geqslant 0\) la taille du tableau.

• Initialisation : Si \(n \leqslant 1\), alors la fonction renvoie le tableau qui est déjà trié et donc elle est correcte
• Hérédité : On appelle la fonction sur un tableau de taille \(n>1\). On suppose que la fonction est correcte pour tous les tableaux de taille \(<n\).
  • Les deux appels récursifs de l'étape Résoudre sont effectués sur des sous-tableaux de taille \(\leqslant n/2\) donc renvoient ces sous-tableaux triés par hypothèse de récurrence forte.
  • L'appel de la fonction fusion fusionne correctement les deux sous-tableaux d'après l'exercice 5.
  • On en déduit que l'appel de la fonction tri_fusion sur le tableau de taille \(n\) renvoie correctement le tableau trié.

Par récurrence forte, on en déduit que la fonction est correcte pour tous les tableaux de taille \(n \geqslant 0\).

Question 4 : complexité du tri fusion

On donne ci-dessous le schéma d'exécution du tri fusion du tableau [7, 5, 3, 0, 1, 6, 4, 2] extrait du document d'accompagnement Eduscol

schéma tri fusion

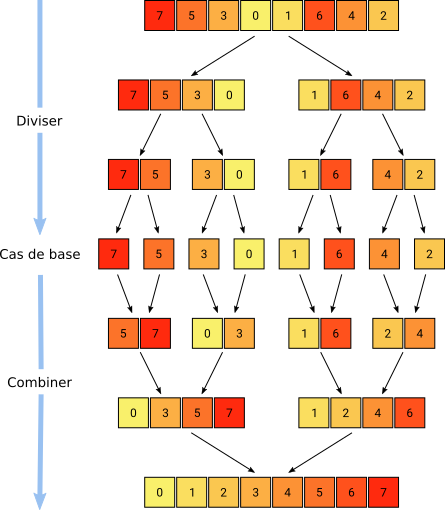
Avec une bonne implémentation, on peut considérer que les phases de l'étape Diviser ne coûtent rien (simples calculs d'indices). Le coût de l'algorithme repose alors entièrement sur les étapes Résoudre et Combiner. Dans le schéma, on peut observer qu'on a plusieurs niveaux de fusion. Pour chaque niveau, la fonction fusion est appelée sur tous les sous-tableaux déjà triés et l'ensemble des éléments du tableau initial est impliqué dans exactement une fusion.

énoncésolution

1. Combien de niveaux de fusion (au plus) sont nécessaires pour trier un tableau de \(8\) éléments ? et pour un tableau de \(16\) éléments ? de \(n\) éléments ?
2. Combien d'éléments sont ajoutés à un nouveau sous-tableau trié par étage de fusion ?
3. En déduire la complexité globale des étapes Résoudre et Combiner et donc du tri fusion.

1. Réponses à la question 1.

   • Il faut 3 niveaux de fusion pour trier un tableau de \(8=2^{3}\) éléments.
   • Il faudra 4 niveaux de fusion pour trier un tableau de \(16=2^{4}\) éléments.
   • Il faudra au plus \(\lceil \log_{2}(n) \rceil\) (\(\log_{2}(n)\) arrondi à l'entier supérieur) niveaux de fusion pour trier un tableau de \(n=2^{\log_{2}(n)}\) éléments. En effet, il y a autant de niveaux de fusion que de niveaux de division par 2. Et il en faut \(\lceil \log_{2}(n) \rceil\) pour fragmenter le tableau initial en sous-tableaux de taille 1.

2. Pour chaque niveau de fusion, les différents appels de la fonction fusion impliquent tous les éléments du tableau initial, chacun est ajouté à un nouveau sous-tableau trié. On a vu que la complexité de fusion(t1, t2) est en \(O(n1+n2)\), donc l'ensembles des fusions sur un même niveau est de complexité linéaire, en \(O(n)\).

3. On a environ \(\log_{2}(n)\) niveaux de fusion avec une même complexité de \(O(n)\) pour chacun, donc globalement on a une complexité de \(O(n\log_{2}(n))\).

Point de cours 3

La complexité en temps du tri fusion d'un tableau de taille \(n\) est linéarithmique, en \(O(n \log_{2}(n))\).

Cette complexité est optimale pour les tris par comparaison de deux éléments.

Le tri fusion est plus efficace que les algorithmes de tri vus en classe de première qui sont de complexité quadratique, en \(O(n^{2})\). Le tri rapide est un autre algorithme Diviser pour Régner, très efficace. L'implémentation, plus délicate, sera vue en TP.

Algorithme de tri d'un tableau de taille \(n\)	Complexité dans le meilleur des cas	Complexité dans le cas moyen	Complexité dans le pire des cas
tri par sélection	\(O(n^{2})\)	\(O(n^{2})\)	\(O(n^{2})\)
tri par insertion	\(O(n)\) (tableau déjà trié)	\(O(n^{2})\) (ordre inverse)	\(O(n^{2})\)
tri par bulles	\(O(n^{2})\)	\(O(n^{2})\)	\(O(n^{2})\)
tri fusion	\(O(n\log_{2}(n))\)	\(O(n\log_{2}(n))\)	\(O(n\log_{2}(n))\)
tri rapide	\(O(n\log_{2}(n))\)	\(O(n\log_{2}(n))\)	\(O(n^{2})\) (tableau déjà trié)

Source : https://www.hackerearth.com/practice/notes/sorting-and-searching-algorithms-time-complexities-cheat-sheet/

Tri fusion en place avec coût linéaire en espace

Exercice 7

On va reprogrammer deux fonctions fusion_place et tri_fusion_place pour réaliser un tri fusion en place d'un tableau d'entiers tab, c'est-à-dire qu'on redistribue les éléments directement dans le tableau, sans les copier vers d'autres tableaux (ce que fait un découpage en tranches). Néanmoins, lors d'une fusion de deux sous-tableaux, on ne peut pas écrire la séquence fusionnée à la place des deux sous-tableaux en cours de traitement : on la stockera dans un tableau auxiliaire et on peut prendre le même pour chaque fusion. On améliore la complexité spatiale par rapport à l'implémentation précédente, on évite les recopies des découpages en tranches et on peut parler de tri fusion en place avec coût linéaire en espace.

Question 1

Dans l'algorithme de tri fusion, on fusionne des sous-tableaux adjacents dans le tableau initial tab, donc il est possible d'identifier deux sous-tableaux par les indices de leurs limites dans tab et comme ils sont adjacents, trois suffisent :

• [g, m[ pour le premier sous-tableau
• [m, d[ pour le suivant

Ainsi on identifiera toujours un sous-tableau par un intervalle d'indices semi-ouvert à droite, comme pour range.

L'algorithme pour fusionner les deux sous-tableaux (par exemple le bleu et le rouge ci-dessous) est le même que celui vu dans l'exercice 5, mais on fusionne d'abord les sous-tableaux t1 = tab[g:m] et t2 = tab[m:d] en insérant les éléments fusionnés toujours dans le même tableau t3 = aux.

Ce dernier est passé en paramètre à la fonction fusion_place avec tab, g, m et d.

Quand la fusion est terminée, on recopie aux[0:d-g] dans tab entre les indices g inclus et d exclu à la place des deux sous-tableaux fusionnés.

énoncésolution

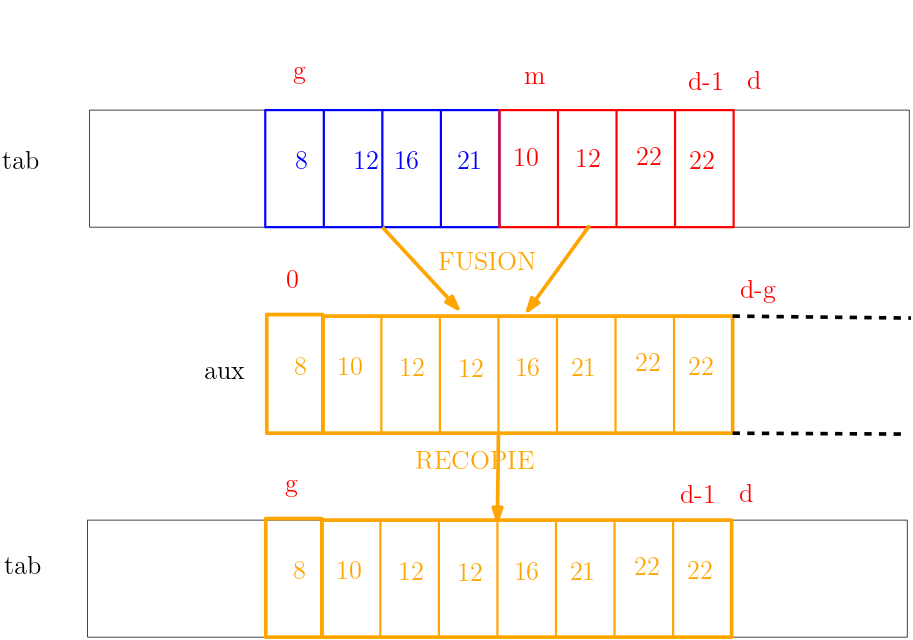
💻 Saisir ses réponses sur Capytale

Complétez la fonction fusion_place dans l'éditeur ci-dessous.

###

Lancer Télécharger Téléverser Recharger Sauvegarder

import randombksl-nlbksl-nldef fusionpy-undplace(tab, g, m, d, aux):bksl-nl """bksl-nl Fusionne les sous-tableaux tab[g:m] et tab[m:d] bksl-nl triés dans l'ordre croissant en un sous-tableau tab[g:d]bksl-nl dans l'ordre croissant. bksl-nl bksl-nl Parameters :bksl-nl tab : tableau d'entiersbksl-nl g, m, d : trois entiersbksl-nl aux : tableau d'entiers pour stocker provisoirementbksl-nl le tableau fusionné dans l'ordre croissantbksl-nl Préconditions : bksl-nl tab[g:m] et tab[m:d] dans l'ordre croissantbksl-nl 0 <= g < m < d <= len(tab)bksl-nl len(tab) <= len(aux)bksl-nlbksl-nl Returns: Nonebksl-nl """bksl-nl assert 0 <= g <= m <= d <= len(tab)bksl-nl assert len(tab) <= len(aux)bksl-nl i1 = g # indice dans tab[g:m]bksl-nl i2 = m # indice dans tab[m:d]bksl-nl i3 = 0 # indice dans auxbksl-nl while i1 < m and ...:bksl-nl if tab[i1] <= tab[i2]:bksl-nl aux[i3] = tab[i1]bksl-nl i1 = i1 + 1bksl-nl else:bksl-nl # à compléterbksl-nl ...bksl-nl i3 = i3 + 1bksl-nl # à compléterbksl-nl ...bksl-nl # on recopie aux dans tab[debut:fin]bksl-nl for k in range(g, d):bksl-nl tab[k] = aux[k - g]bksl-nlbksl-nl bksl-nldef testpy-undfusionpy-undplace():bksl-nl aux = [0 for py-und in range(8)]bksl-nl # test 1 : tableau fusionné = tableau completbksl-nl t1 = [1, 10, 20, 5, 8, 9, 15, 25]bksl-nl fusionpy-undplace(t1, 0, 3, 8, aux)bksl-nl assert t1 == [1, 5, 8, 9, 10, 15, 20, 25]bksl-nl # test 2 : tableau fusionné = sous-tableaubksl-nl t2 = [50, 10, 20, 5, 22, 30, 7, 4]bksl-nl fusionpy-undplace(t2, 1, 3, 6, aux)bksl-nl assert t2 == [50, 5, 10, 20, 22, 30, 7, 4]bksl-nl # test 3 : fusion de deux sous-tableaux avec un élémentbksl-nl t3 = [50, 40, 20, 15, 7]bksl-nl fusionpy-undplace(t3, 1, 2, 3, aux)bksl-nl assert t3 == [50, 20, 40, 15, 7]bksl-nl # test 4 : fusion avec deux sous-tableaux touchant un bordbksl-nl t4 = [50, 12, 18, 10, 15, 17]bksl-nl fusionpy-undplace(t4, 1, 3, 6, aux)bksl-nl assert t4 == [50, 10, 12, 15, 17, 18]bksl-nl print("tests réussis")bksl-nl bksl-nl bksl-nldef tripy-undfusionpy-undplace(tab, g, d, aux):bksl-nl """bksl-nl Tri fusion en place et récursif de tab[g;d]bksl-nl avec aux comme tableau auxilaire de stockage pour la fusionbksl-nlbksl-nl Parametersbksl-nl ----------bksl-nl tab : tableau d'entiersbksl-nl g, d : deux entiersbksl-nl aux : tableau d'entiersbksl-nl bksl-nl Préconditions :bksl-nl 0 <= g < d <= len(tab)bksl-nl len(aux) >= len(tab)bksl-nl Returnsbksl-nl -------bksl-nl None.bksl-nl """bksl-nl # Préconditionsbksl-nl assert 0 <= g <= d <= len(tab)bksl-nl assert len(aux) >= len(tab)bksl-nl n = d - gbksl-nl if n <= 1: # cas de base : tableau à 1 élément déjà triébksl-nl returnbksl-nl else: # appels récursifsbksl-nl # Diviserbksl-nl m = (g + d) // 2 bksl-nl # Résoudre les deux sous-problèmesbksl-nl # à compléterbksl-nl ...bksl-nl # Combiner les solutionsbksl-nl # à compléterbksl-nl ...bksl-nl bksl-nldef tripy-undfusionpy-undplacepy-undenveloppe(tab):bksl-nl """bksl-nl Fonction enveloppe pour tri fusion en place du tableau d'entiers tabbksl-nl """bksl-nl tripy-undfusionpy-undplace(..., ..., ..., ...)bksl-nlbksl-nldef testpy-undtripy-undfusionpy-undplace():bksl-nl for taille in range(10):bksl-nl for py-und in range(20):bksl-nl tab = [random.randint(0, taille) for py-und in range(taille)]bksl-nl aux = [0 for py-und in range(taille)]bksl-nl tripy-undfusionpy-undplace(tab, 0, taille, aux)bksl-nl assert tab == sorted(tab)bksl-nl print("tests réussis")bksl-nl

🐍 Script Python

def fusion_place(tab, g, m, d, aux):
    """
    Fusionne les sous-tableaux tab[g:m] et tab[m:d]  
    triés dans l'ordre croissant en un sous-tableau tab[g:d]
    dans l'ordre croissant. 
    
    Parameters :
    tab : tableau d'entiers
    g, m, d : trois entiers
    aux : tableau d'entiers pour stocker provisoirement
        le tableau fusionné dans l'ordre croissant
    Préconditions : 
        tab[g:m] et tab[m:d]  dans l'ordre croissant
        0 <= g < m < d <= len(tab)
        len(tab) <= len(aux)

    Returns:  None
    """
    assert 0 <= g <= m <= d <= len(tab)
    assert len(tab) <= len(aux)
    i1 = g # indice dans tab[g:m]
    i2 = m  # indice dans tab[m:d]
    i3 = 0 # indice dans aux
    while i1 < m and i2 < d:
        if tab[i1] <= tab[i2]:
            aux[i3] = tab[i1]
            i1 = i1 + 1
        else:
            aux[i3] = tab[i2]
            i2 = i2 + 1
        i3 = i3 + 1
    while i1 < m:
        aux[i3] = tab[i1]
        i1 = i1 + 1
        i3 = i3 + 1
    while i2 < d:
        aux[i3] = tab[i2]
        i2 = i2 + 1
        i3 = i3 + 1
    # on recopie aux dans tab[debut:fin]
    for k in range(g, d):
        tab[k] = aux[k - g]

Question 2

énoncésolution

💻 Saisir ses réponses sur Capytale

Dans l'éditeur précédent :

• Complétez la fonction tri_fusion_place qui trie en place un tableau d'entiers tab avec l'algorithme de tri_fusion à l'aide de la fonction fusion_place. Cette fonction ne renvoie rien (tri en place) mais prend trois autres arguments en plus du tableau à trier.
• Complétez alors la fonction tri_fusion_place_enveloppe qui ne prend qu'un seul argument tab, le tableau à trier, et appelle tri_fusion_place avec les bons arguments.

🐍 Script Python

def tri_fusion_place(tab, g, d, aux):
    """
    Tri fusion en place et récursif de tab[g;d]
    avec aux comme tableau auxilaire de stockage pour la fusion

    Parameters
    ----------
    tab : tableau d'entiers
    g, d : deux entiers
    aux : tableau d'entiers
    
    Préconditions :
        0 <= g < d <= len(tab)
        len(aux) >= len(tab)
    Returns
    -------
    None.
    """
    # Préconditions
    assert 0 <= g <= d <= len(tab)
    assert len(aux) >= len(tab)
    n = d - g
    if n <= 1:  # cas de base : tableau à 1 élément déjà trié
        return
    else:  # appels récursifs
        # Diviser
        m = (g + d) // 2       
        # Résoudre les deux sous-problèmes
        tri_fusion_place(tab, g, m, aux)
        tri_fusion_place(tab, m, d, aux)
        # Combiner les solutions
        fusion_place(tab, g, m, d, aux)

def tri_fusion_place_enveloppe(tab):
    """
    Fonction enveloppe pour tri fusion en place du tableau d'entiers tab
    """
    tri_fusion_place(tab, 0, len(tab), [0 for _ in range(len(tab))])