version pdf

Synthèse du cours Algorithmes gloutons

Solution approchée d'un problème d'optimisation et heuristique gloutonne

Problème du voyageur de commerce (Travelling Salesman Problem)

William Rowan Hamilton a posé pour la première fois ce problème, dès 1859. Sous sa forme la plus classique, son énoncé est le suivant :

Un voyageur de commerce doit visiter une et une seule fois un nombre fini de villes et revenir à son point d'origine. Trouvez l'ordre de visite des villes qui minimise la distance totale parcourue par le voyageur

Il s'agit d'un problème d'optimisation dont la spécification est la suivante :

• Entrée du problème : une liste de villes reliées deux à deux et le tableau des distances entre deux villes
• Sortie du problème : un cycle passant une fois et une seule par chaque ville avec retour à la ville de départ, telle que la distance totale, somme des distances séparant deux étapes successives, soit minimale.

On peut modéliser l'entrée du problème par un graphe pondéré dont les sommets sont les villes et les arêtes les liaisons entre les villes. Nous nous restreindrons au cas d'un graphe complet : chaque ville est reliée à toutes les autres.

Résoudre le problème du voyageur de commerce revient à trouver dans ce graphe un cycle passant par tous les sommets une unique fois (un tel cycle est dit hamiltonien) et qui soit de longueur minimale.

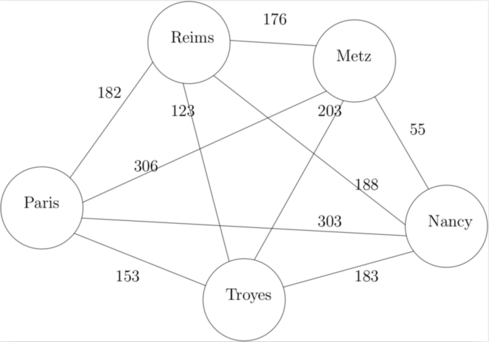
Heuristique gloutonne et algorithme glouton

On a vu qu'une recherche exhaustive peut résoudre de façon exacte le problème du voyageur de commerce mais ne peut pas être utilisée en pratique puisque par explosion combinatoire, la complexité de l'algorithme force brute est pire qu'exponentielle, en \(O(n!)\).

Si une solution exacte n'est pas accessible en un temps raisonnable, une bonne solution approchée peut être acceptable et même parfois s'avérer exacte ! On désigne par heuristique une méthode de résolution approchée.

Dans le problème du voyageur de commerce, un circuit solution est constitué d'une séquence de villes. On peut imaginer construire une solution approchée en insérant à chaque étape la ville qui fait le moins augmenter la longueur totale du circuit en cours. Une telle heuristique qui essaie d'approcher une solution globalement optimale par une succession de choix localement optimaux, s'appelle une heuristique gloutonne.

Un algorithme qui construit une solution avec une heuristique gloutonne est un algorithme glouton.

Si on a un problème d'optimisation dont une solution peut être construite itérativement mais pour lequel on ne connaît pas d'algorithme de résolution exacte efficace, alors un algorithme glouton peut être intéressant :

Caractéristiques d'un algorithme glouton

• Un algorithme glouton construit une solution par une succession de choix localement optimaux, en espérant obtenir une solution globalement optimale
• Un algorithme glouton est efficace, car il progresse directement vers une solution sans jamais remettre en question les choix précédents. Sa complexité est souvent facile à établir. Le travail pour effectuer chaque choix glouton est souvent effectué lors d'un prétraitement, par exemple avec un tri de l'entrée.
• Un algorithme glouton n'est pas toujours correct, et s'il l'est, la preuve peut être difficile.

Différences entre algorithmes Glouton et Diviser Pour Régner

Thème	Algorithme glouton	Algorithme Diviser Pour Régner
Difficulté de conception	Facile	Difficile
Complexité	Facile à établir	Difficile à établir
Correction	Difficile à prouver	Facile à prouver (par récurrence)

Problème difficile

Les problèmes que nous avons résolus par un algorithme (tri, recherche dans un tableau, parcours d'un arbre ...) peuvent être résolus en un nombre d'opérations inférieur à \(n^{p}\), on dit qu'ils appartiennent à la classe de complexité P pour polynomial. Le problème du voyageur de commerce appartient à la classe de complexité NP. Elle correspond aux problèmes pour lesquels les solutions sont faciles à vérifier (la vérification d'une solution peut se faire en un nombre d'opérations polynomial), alors qu'on ne connaît pas d'algorithme de construction d'une solution appartenant à la classe P. Par exemple il est facile de vérifier qu'une solution de grille de Sudoku est correcte mais il est difficile de la trouver.

Un algorithme glouton optimal dans certains cas

Problème du rendu de monnaie

On se place dans la position du caissier qui doit rendre en monnaie un certain montant avec un nombre minimal de pièces. On suppose que le caissier dispose en nombre illimité de toutes les valeurs de pièces disponibles. L'ensemble des valeurs de pièces disponibles constitue le système monétaire.

Il s'agit d'un problème d'optimisation dont la spécification est la suivante :

• Entrée du problème : un montant à rendre et une liste de valeurs de pièces d'un système monétaire ; on suppose qu'on dispose d'un nombre illimité de pièces de chaque valeur

• Sortie du problème : une liste de pièces dont la somme est égale au montant à rendre et dont le nombre de pièces est minimal ; ou une liste vide si le montant ne peut être atteint avec les pièces du système

Algorithme glouton de rendu de monnaie

Comme pour le problème du voyageur de commerce, la recherche exhaustive d'une solution n'est pas raisonnable : il faudrait déterminer toutes les décompositions en somme de pièces de la monnaie à rendre. Une heuristique gloutonne de construction d'une solution est assez naturelle et peut se résumer en une phrase :

• tant qu'il reste un montant à rendre on choisit la plus grande valeur de pièce disponible inférieure ou égale à la somme et on la retranche du montant à rendre

Cet algorithme glouton se termine dès que le système monétaire contient une pièce de valeur 1.

L'optimalité de l'algorithme glouton dépend du système monétaire. Par exemple avec le système monétaire [1, 4, 6] l'algorithme glouton rend le montant 8 avec les pièces[6, 1, 1] ce qui n'est pas optimal car on peut rendre en deux pièces avec [4, 4].

Cependant il existe des systèmes monétaires, dits canoniques, où l'algorithme glouton rend toujours la monnaie en un nombre minimum de pièces. On ne connaît pas de critère simple pour déterminer si un système est canonique mais on peut démontrer que le système de l'euro est canonique. Par ailleurs, on peut s'assurer qu'un système est canonique en vérifiant que l'algorithme glouton est optimal pour toutes les sommes inférieures à la somme des deux pièces de valeurs maximales.

🐍 Script Python

def rendu_glouton(restant, pieces):
    # pieces tableau de valeurs de pièces disponibles dans l'ordre croissant
    indice_pieces = len(pieces) - 1
    rendu = []
    while restant > 0 and  indice_pieces >= 0:
        if pieces[indice_pieces] <= restant:
            restant = restant - pieces[indice_pieces]
            rendu.append(pieces[indice_pieces])
        else:
            indice_pieces = indice_pieces - 1
    # rendu possible
    return rendu

systeme_euro = [1, 2, 5, 10, 20, 50, 100, 200, 500]
assert rendu_glouton(49, systeme_euro) == [20, 20, 5, 2, 2]