Recherche dichotomique dans un tableau trié

Spécification du problème de la recherche dichotomique

• Entrées :

  • Un tableau tab d'éléments du même type et comparables entre eux qui doit vérifier la précondition que le tableau est trié (on suppose dans l'ordre croissant mais il suffira d'inverser les inégalités pour un ordre décroissant).
  • Un élément e du même type que ceux de tab et comparables avec tous les éléments de tab

• Sortie :

  • Si e est présent dans tab : l'index d'une occurrence de e dans tab
  • Sinon : une valeur particulière marquant l'absence de e dans tab : -1 ou len(tab) ou None

Recherche dichotomique avec zone de recherche [g; d]

Notons g l'indice de la première case et d l'indice la dernière case de la zone de recherche du tableau tab dans laquelle on recherche l'élément e. On initialise g avec 0 et d avec len(tab) - 1.

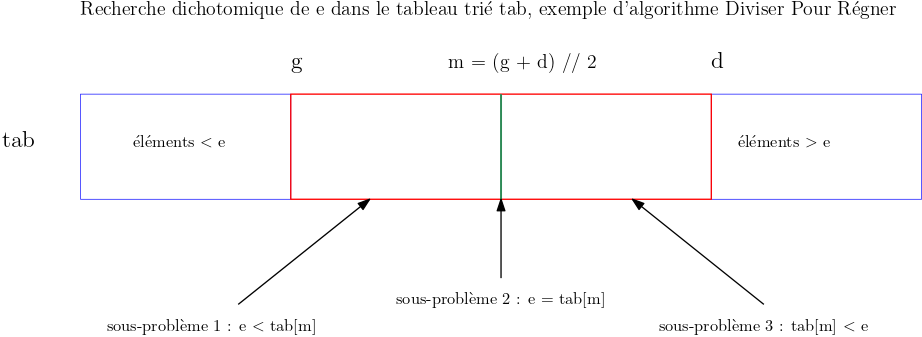
On applique la méthode Diviser Pour Régner :

• Diviser : on divise le tableau tab par sa position médiane m
• Résoudre : on pose une question sur l'élément tab[m] : est-il plus grand, égal ou plus petit que e ?
  • si e < tab[m] on continue la recherche dans la première moitié du tableau qui correspond à l'intervalle d'indices [g; m - 1]
  • sinon si e == tab[m] on peut renvoyer m comme réponse au problème
  • sinon si tab[m] < e on continue la recherche dans la seconde moitié du tableau qui correspond à l'intervalle d'indices [m + 1; d]

Recherche dichotomique itérative (avec une boucle)

🐍 Script Python

def recherche_dicho(tab, elt):
    g = 0
    d = len(tab) - 1
    while g <= d:
        m = (g + d) // 2
        if tab[m] < elt:
            g = m + 1
        elif tab[m] > elt:
            d = m - 1
        else:
            return m
    return -1

Recherche dichtomique récursive (TNSI)

🐍 Script Python

def dicho_rec(tab, elt, g, d):
    if g > d: # cas de base : zone de recherche vide
        return -1
    m = (g + d) // 2
    if tab[m] == elt:  # cas de base : élément trouvé
        return m
    elif tab[m] < elt:
        return dicho_rec(tab, elt, m + 1, d)
    else:  # sous-problème 2  tab[m] > elt:
        return dicho_rec(tab, elt, g, m - 1)


def recherche_dicho(tab, elt):
    """Fonction enveloppe"""
    return dicho_rec(tab, elt, 0, len(tab) - 1)

L'algorithme se termine-t-il ?

L'algorithme ne se terminerait pas si la boucle while non bornée était infinie.

Supposons qu'on n'ait jamais tab[m] == elt et donc pas des sortie prématurée dans la boucle while non bornée.

Pour démontrer que la boucle se termine, on utilise la quantité d - g qui vérifie les propriétés suivantes :

• (P1) : cette quantité reste un entier tout au long de l'exécution
• (P2) : la boucle s'exéxute si et seulement si cette quantité est positive
• (P3) : si la boucle s'exécute alors la quantité diminue strictement au cours de l'itération de boucle : c'est le cas ici puisque soit g <= m devient m + 1 et donc est incrémentée, soit m <= d devient m - 1 et donc est décrémentée

Ces trois propriétés font que chaque itération de boucle s'effectue pour une valeur de d - g entière positive et qui diminue strictement au cours de la progression de la boucle. Or il n'existe pas de suite d'entiers positifs avec une infinité de termes. Par l'absurde on démontre donc que la boucle se termine forcément.

Une quantité vérifiant ces trois propriétés s'appelle un variant de boucle. Elle permet de démontrer la terminaison d'une boucle non bornée.

L'algorithme est-il correct ?

Un algorithme est correct s'il se termine et s'il répond à sa spécification.

Pour démontrer la correction de l'algorithme, on utilise un invariant de boucle : c'est une propriété qui est vraie avant la boucle et qui est préservée par chaque itération de la boucle. On choisit l'invariant pour qu'il donne une réponse correcte selon la spécification de l'algorithme en sortie de boucle.

Ici on distingue deux cas :

• Premier cas : On sort prématurément de la boucle parce que tab[m] == elt en renvoyant m qui est bien une position de elt dans tab et donc l'algorithme est correct.

• Second cas : On ne sort jamais prématurément de la boucle. Dans ce cas on va utiliser un invariant de boucle qui se formule ainsi pour la zone de recherche [g ; d] : > D'une part les éléments de tab d'indice inférieur à g sont strictement inférieurs à l'élément e cherché > D'autre part les éléments de tab d'indice supérieur à d sont strictement supérieurs à l'élément e cherché > Ainsi si e dans tab alors il se trouve forcément dans la zone de recherche [g; d].

  Cette propriété est bien préservée par chaque itération de la boucle :

  • Si t[m] < e alors comme le tableau est trié dans l'ordre croissant tous les éléments d'indice g <= k <= m sont aussi inférieurs à e et donc on peut continuer la recherche dans [m + 1; d] en préservant l'invariant
  • Si t[m]> e alors comme le tableau est trié dans l'ordre croissant tous les éléments d'indice m <= k <= d sont aussi supérieurs e et donc on peut continuer la recherche dans [g ; m - 1] en préservant l'invariant

  En sortie de boucle on a une zone de recherche vide car d < g et tous les éléments du tableau en dehors de la zone de recherche sont différents de e donc il est correct de renvoyer une valeur indiquant que e n'appartient pas au tableau.

L'algorithme est-il efficace ?

A chaque itération de boucle la nouvelle zone de recherche a une taille inférieure ou égale à la moitié de la précédente. Si on cherche dans un tableau de taille \(2^{n}\), dans le pire des cas où l'on cherche un élément qui n'appartient pas au tableau, après \(n+1\) itérations la zone de recherche a une taille inférieure ou égale à \(2^{n}/2^{n+1}=0,5\) donc elle est vide (car sa taille est un entier) et l'algorithme se termine.

Dans ce cas \(n+1\) est le nombre de chiffres de la taille \(2^{n}\) du tableau en binaire. A une constante près c'est le logarithme de cette taille, on parle de coût logarithmique pour une recherche dichotomique.

C'est beaucoup mieux que le coût linéaire (la taille du tableau à une constante près) de la recherche séquentielle : comparez un entier avec son nombre de chiffres, plus l'entier est grand plus l'écart est important !

⚠️ La recherche dichotomique n'est possible que sur un tableau trié !

Recherche dichotomique avec zone de recherche [g; d [ (semi-ouvert à droite)

g désigne toujours l'indice de la première case mais d est l'indice suivant la dernière case de la zone de recherche du tableau tab dans laquelle on recherche l'élément e. On initialise g avec 0 et d avec len(tab).

⚠️ A la différence de la première méthode, la borne droite de la zone de recherche n'en fait pas partie.

On applique la méthode Diviser Pour Régner :

• Diviser : on divise le tableau tab par sa position médiane m
• Résoudre : on pose une question sur l'élément tab[m] : est-il plus grand, égale ou plus petit que e ?
  • si e < tab[m] on continue la recherche dans la première moitié du tableau qui correspond à l'intervalle d'indices [g; m [
  • sinon si e == tab[m] on peut renvoyer m comme réponse au problème
  • sinon si tab[m] < e on continue la recherche dans la seconde moitié du tableau qui correspond à l'intervalle d'indices [m + 1; d[

Recherche dichtomique itérative (avec zone de recherche [g; d[ )

🐍 Script Python

def recherche_dicho(tab, elt):
    g = 0
    d = len(tab)
    while g < d: # la condition de sortie boucle change car la zone de recherche est [g; d[ et plus [g; d]
        # Invariant : tab[k] < elt si k < g  et t[k] > elt si k >= d
        m = (g + d) // 2
        if tab[m] < elt:
            g = m + 1
        elif tab[m] > elt:
            d = m
        else:
            return m
    return -1

Recherche dichotomique de la dernière occurrence d'un élément dans un tableau trié¶

Spécification du problème

• Entrées :

  • Un tableau tab d'éléments du même type et comparables entre eux qui doit vérifier la précondition que le tableau est trié (on suppose dans l'ordre croissant mais il suffira d'inverser les inégalités pour un ordre décroissant).
  • Un élément e du même type que ceux de tab et comparables avec tous les éléments de tab

• Sortie :

  • Si e est présent dans tab : l'index de la dernière occurrence de e dans tab
  • Sinon : une valeur particulière marquant l'absence de e dans tab : -1 ou len(tab) ou None

⚠️ Contrairement à la recherche dichotomique, on ne veut pas l'index une occurrence quelconque mais l'index particulier de la dernière occurrence ! On parle de recherche du point d'insertion dichotomique parce que par exemple on souhaite insérer un 2 après sa dernière occurrence.

Par exemple, ci-dessous recherche_dicho ne nous renvoie pas l'index de la dernière occurrence d'un 2 dans t :

🐍 Script Python

>>> t = [1, 1, 2, 2, 2, 2, 2, 3]
>>> recherche_dicho(t, 2)
>>> 3

Recherche dichotomique de la dernière occurrence

On considère une zone de recherche semi-ouverte à droite [g; d[. On souhaite que si e dans tab, la zone de recherche contienne au moins une occurrence de e mais pas forcément toutes. On peut donc se contenter d'un invariant moins fort que pour la recherche dichotomique :

D'une part tab[g] <= e D'autre part les éléments de tab d'indice supérieur ou égal à d sont strictement supérieurs à l'élément e cherché Ainsi sie dans tab qui est trié dans l'ordre croissant, on aura au moins une occurrence dans la zone de recherche [g;d[.

On applique la méthode Diviser Pour Régner :

• Diviser : on divise le tableau tab par sa position médiane m
• Résoudre : on pose une question plus simple sur l'élément tab[m] : est-il inférieur ou égal à e ?
  • si tab[m] <= e on continue la recherche dans la seconde moitié du tableau qui correspond à l'intervalle d'indices [m; d[
  • sinon e < tab[m] et on continue la recherche dans la première moitié du tableau qui correspond à l'intervalle d'indices [g;m[

Différences avec la recherche dichotomique :

• On doit aller jusqu'au bout de la dichotomie, c'est-à-dire jusqu'à ce que la zone de recherche ne contienne plus qu'un seul élément. Si e dans tab, la préservation de l'invariant garantira que d'une part il sera dans [g;d[ et d'autre part tous les éléments d'indice >= d seront supérieurs à e donc on aura capturé la dernière occurrence de e.
• On sort donc de la boucle lorsqu'il ne reste plus qu'un élément dans la zone de recherche d'où la condition d'entrée de boucle : while d - g > 1.
• Lors des réductions de la zone de recherche on remplace g ou d par m (pas de m -1 ou m +1), ce choix est dicté par la préservation de notre invariant (tab[g] <= e et si k >= d alors e < tab[k])

Exemple :

🐍 Script Python

>>> t = [1, 1, 2, 2, 2, 2, 2, 3]
>>> recherche_dicho_dernier(t, 2)
>>> 6

Recherche dichotomique de la dernière occurrence

🐍 Script Python

def recherche_dicho_dernier(tab, e):
    g = 0
    d = len(tab)
    while d - g > 1:  # tant qu'il y a au moins deux éléments dans la zone de recherche
        # Invariant : tab[g] <= e et   si k >= d alors e < tab[k]
        m = (g + d) // 2
        if tab[m] <= e:
            g = m
        else:
            d = m
    if tab[g] == e:
        return g  # position de la dernière occurrence de elt dans tab
    else:
        return -1  # l'élément n'est pas dans tab