Aller au contenu

Avantages et défauts de la récursivité (Bac 🎯)⚓︎

Licence Creative Commons
Ce cours est mis à disposition selon les termes de la Licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.

programme

Sources et crédits pour ce cours

Pour préparer ce cours, j'ai utilisé :

🔖 Synthèse de ce qu'il faut retenir pour le bac

Plusieurs cas de base⚓︎

Exercice 4

Exercice tiré de la ressource ressource Eduscol sur la récursivité

Problème : On dispose de briques de longueur 2 ou 3. Combien de murs de longueur \(n\) distincts peut-on construire avec ces briques ?

Voici par exemple les trois solutions possibles pour des rangées de longueur 7 : (chaque brique est symbolisée par une couleur différente).

Ainsi il y a 3 façons de construire un mur de longueur 7 : 223 232 322

mur

  1. Déterminez le nombre de façons de construire un mur de longueur \(8\).
  2. On note murs(n) le nombre de façons de construire un mur de longueur \(n\). Comment peut-on réduire le calcul de murs(n) à des calculs similaires mais pour des murs de longuers inférieures ?
  3. Combien de murs de longueur 0 peut-on construire ? et de longueur 1, 2 ou 3 ?
  4. Écrire une fonction récursive murs qui résout le problème.

###
def murspy-undenveloppe(n):bksl-nl """bksl-nl Fonction enveloppe qui vérifie une précondition sur nbksl-nl On évite ainsi de vérifier la précondition pourchaque appel récursifbksl-nl """bksl-nl assert isinstance(n, int) and n >= 0, "la longeur n doit être un entier positif"bksl-nl return murs(n)bksl-nlbksl-nldef murs(n):bksl-nl """Fonction récursive"""bksl-nl # cas de base à compléterbksl-nl # réduction et appels récursifs bksl-nlbksl-nl

🐍 Script Python
def murs_enveloppe(n):
    assert isinstance(n, int) and n >= 0, "la longeur n doit être un entier positif"
    return murs(n)

def murs(n):    
    if n <= 1:
        return 0
    if n == 2 or n == 3:
        return 1
    return murs(n - 2) + murs(n - 3)

Point de cours 3

Dans l'exercice précédent, on a vu un exemple où la récursivité permet d'exprimer simplement et lisiblement une solution à un problème en ramenant sa résolution à la résolution de problèmes similaires mais plus petits. Cette approche sera déclinée dans les méthodes de résolution :

  • Diviser pour régner où les sous-problèmes sont indépendants
  • par Programmation dynamique où les sous-problèmes peuvent se chevaucher, comme dans l'exercice 4.

Récursivité multiple⚓︎

Exemple 6

La suite de Fibonacci, est définie récursivement : chaque nouvelle valeur est la somme des deux dernières valeurs calculées. Évidemment il faut partir de valeurs initiales qui sont 0 et 1.

Mathématiquement si on note \((f_{n})\) la suite alors on peut la définir pour tout entier naturel \(n\) par :

  • \(f_{0}=0\) et \(f_{1}=1\)
  • \(f_{n}=f_{n-1}+f_{n-2}\) pour tout entier \(n \geqslant 2\)

Il est naturel de traduire cette définition sous la forme d'une fonction récursive, pour calculer le terme de rang \(n\) de la suite.

Les deux cas de base \(n=0\) et \(n=1\) peuvent être regroupés dans une seule conditionnelle mais la partie réduction doit comporter deux appels récursifs. On parle dans ce cas de récursivité multiple.

🐍 Script Python
def fibo(n):
    """Fonction enveloppe pour ne vérifier la précondition sur n qu'une seule fois"""
    assert isinstance(n, int) and n >= 0
    return fibo_rec(n)

def fibo_rec(n):
    if n <= 1:  # 2 cas de bases n = 0 ou n = 1
        return n
    return fibo_rec(n - 1) + fibo_rec(n - 2)

Exercice 5

🎯 Analyser le fonctionnement d'un programme récursif

  1. Représentez l'arbre d'appels pour le calcul de fibo_rec(3) puis pour le calcul de fibo_rec(5).

  2. Exécutez le code ci-dessous. Quelle conjecture peut-on faire sur l'évolution du temps d'exécution de fibo_rec(n) lorsque \(n\) augmente \(1\) ? Est-il raisonnable d'envisager le calcul de fibo_rec(20) ?

    Attention

    Si on exécute ce code sur Capytale, on peut calculer des valeurs plus grandes, et le ratio entre les temps de calcul de fibo_rec(n) et fibo_rec(n+1) tend vers \(1,6\) ce qui correspond mieux à la théorie. Pour autant, même avec une technologie ou une machine plus performante, peut-on calculer avec cet algorithme une valeur comme fibo_rec(50) ?

    📋 Texte
    n= 15  f(n)= 610  Temps= 0.0010001659393310547  Ratio= 0.0010001659393310547
n= 16  f(n)= 987  Temps= 0.0019998550415039062  Ratio= 1.999523241954708
n= 17  f(n)= 1597  Temps= 0.002000093460083008  Ratio= 1.0001192179303768
n= 18  f(n)= 2584  Temps= 0.0039997100830078125  Ratio= 1.9997615925616878
n= 19  f(n)= 4181  Temps= 0.006000041961669922  Ratio= 1.5001192179303768
n= 20  f(n)= 6765  Temps= 0.010999917984008789  Ratio= 1.833306842565366
n= 21  f(n)= 10946  Temps= 0.01699995994567871  Ratio= 1.5454624271192319
n= 22  f(n)= 17711  Temps= 0.0280001163482666  Ratio= 1.6470695482658513
n= 23  f(n)= 28657  Temps= 0.045999765396118164  Ratio= 1.6428419376538006
n= 24  f(n)= 46368  Temps= 0.07300019264221191  Ratio= 1.58696880328812
n= 25  f(n)= 75025  Temps= 0.11999988555908203  Ratio= 1.6438297107957607
n= 26  f(n)= 121393  Temps= 0.1919999122619629  Ratio= 1.6000007947293549
n= 27  f(n)= 196418  Temps= 0.3100001811981201  Ratio= 1.6145850148887504
n= 28  f(n)= 317811  Temps= 0.502000093460083  Ratio= 1.6193541936649913
n= 29  f(n)= 514229  Temps= 0.8119997978210449  Ratio= 1.61752917658692
n= 30  f(n)= 832040  Temps= 1.317000150680542  Ratio= 1.6219217716736343

    ###
    import timebksl-nlbksl-nldef fibopy-undrec(n):bksl-nl if n <= 1:bksl-nl return nbksl-nl else:bksl-nl return fibopy-undrec(n - 1) + fibopy-undrec(n - 2) bksl-nlbksl-nltp = 1bksl-nlfor n in range(5, 11):bksl-nl debut = time.time()bksl-nl fn = fibopy-undrec(n)bksl-nl t = time.time() - debutbksl-nl print("n=", n, " f(n)=", fn, " Temps=", time.time() - debut, " Ratio=", t/tp)bksl-nl tp = tbksl-nl

  3. Il est frustrant de ne pas pouvoir calculer des valeurs comme fibo_rec(50).

    a. Écrivez une version itérative fibo_iter qui peut calculer à l'aide d'une boucle des valeurs fibo_iter(n) pour des valeurs de \(n\) plus grandes.

    b. Dans ce cas la lisibilité va-t-elle de pair avec l'efficacité ?

    ###
    bksl-nlbksl-nlbksl-nl

  4. À partir des arbres d'appels déjà réalisés et de celui pour fibo_rec(5), quelle explication peut-on donner pour les performances médiocres de la fonction récursive fibo_rec par rapport à la fonction itérative fibo_iter ?

    Arbre d'appels pour fibo_rec(5)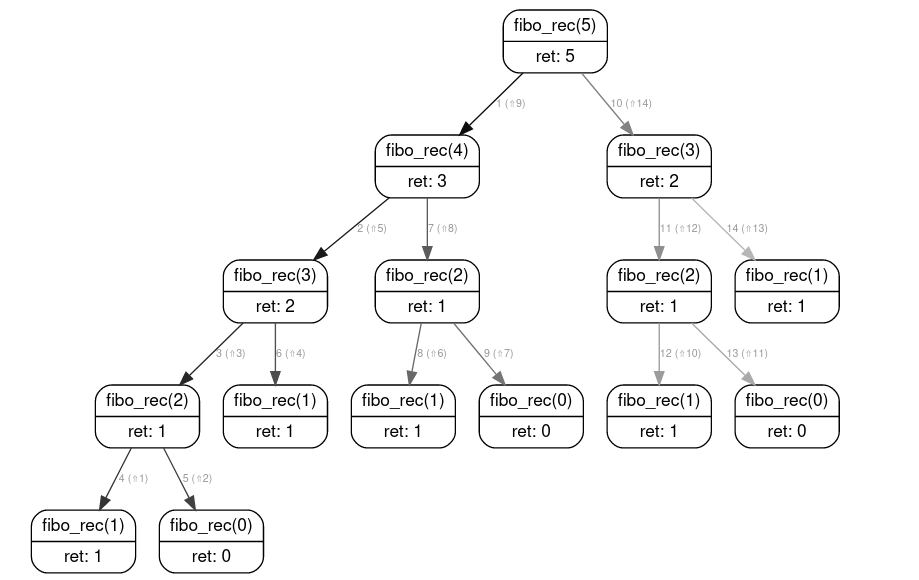

    arbre5

    On pose \(c(n)\) le coût en opérations de l'exécution de fibo_rec(n). De plus on pose \(c(0)=c(1)=1\).

    a. Quelle relation de récurrence permet d'exprimer \(c(n)\) ?

    b. D'après la page Wikipedia sur la suite de Fibonacci, en déduire une estimation de \(c(n)\).

    c. Comparez avec la complexité de la fonction itérative fibo_iter.

Point de cours 4

Si une fonction récursive permet d'exprimer une solution à un problème de façon plus lisible et élégante qu'une fonction itérative, il faut se méfier de la complexité cachée. En général la complexité \(c(n)\) en fonction de la taille \(n\) de l'entrée, peut s'exprimer à l'aide d'une relation de récurrence.

Par exemple, des récurrences de la forme \(c(n+1)= 2 c(n)\) ou \(c(n+2)=c(n)+c(n+1)\) conduisent à des complexité exponentielles en \(c(n) \approx k \times q^{n}\) avec \(q>1\).

Modèle d'exécution d'une fonction récursive⚓︎

Exercice 6

  1. Complétez les fonctions somme_rec et somme_iter dans l'IDE ci-dessous. Ces deux fonctions doivent calculer pour un entier \(n \geqslant 1\), la somme \(\sum_{k=1}^{n}k\) avec une répétition (appels récursifs ou boucle).

    ###
    #--- HDR ---#bksl-nlDICOpy-undTRACE = dict()bksl-nlbksl-nlbksl-nldef trace(f):bksl-nl """Remplace une fonction f par une fonction enrobante g."""bksl-nlbksl-nl def g(py-strargs):bksl-nl """Fonction enrobante (wraped en anglais)."""bksl-nl arguments = f"{args[0]}"bksl-nl bksl-nl if g.tracepy-undpile:bksl-nl g.pile.append(f"Contexte de {g.py-undpy-undnamepy-undpy-und}{tuple(e for e in args)}")bksl-nl lmax = max([len(contexte) for contexte in g.pile])bksl-nl print(f"Appel de {g.py-undpy-undnamepy-undpy-und}({arguments}) => descente \n")bksl-nl print("État de la pile : \n")bksl-nl for contexte in g.pile[::-1]:bksl-nl print("|{0:^{1}}|".format(contexte, lmax))bksl-nl print(f"|{lmax py-str '-'}|")bksl-nl print("\n" py-str 3 )bksl-nl if not(g.tracepy-undpile) and g.trace:bksl-nl print(bksl-nl "| " py-str (g.indentation - 1)bksl-nl + "┌"bksl-nl + f"Appel de {g.py-undpy-undnamepy-undpy-und}({arguments}) => descente"bksl-nl )bksl-nl g.indentation += 1bksl-nl g.py-undpy-unddictpy-undpy-und["indentation"] = g.indentationbksl-nl retour = f(py-strargs)bksl-nl if not(g.tracepy-undpile) and g.trace:bksl-nl g.indentation -= 1bksl-nl g.py-undpy-unddictpy-undpy-und["indentation"] = g.indentationbksl-nl print(bksl-nl "| " py-str (g.indentation - 1)bksl-nl + "└"bksl-nl + f"Fin de {g.py-undpy-undnamepy-undpy-und}({arguments}) <= remontée"bksl-nl )bksl-nl if g.tracepy-undpile: bksl-nl print(f"Fin de {g.py-undpy-undnamepy-undpy-und}({arguments}) <= remontée \n")bksl-nl lmax = max([len(contexte) for contexte in g.pile])bksl-nl print("État de la pile : \n")bksl-nl for contexte in g.pile[::-1]:bksl-nl print("|{0:^{1}}|".format(contexte, lmax))bksl-nl print(f"|{lmax py-str '-'}|")bksl-nl print("\n" py-str 2 )bksl-nl g.pile.pop()bksl-nl return retourbksl-nlbksl-nl # on vérifie si le nom de f apparaît déjà dans table des fonctions tracéesbksl-nl if f.py-undpy-undnamepy-undpy-und not in DICOpy-undTRACE:bksl-nl g.py-undpy-undnamepy-undpy-und = f.py-undpy-undnamepy-undpy-und # g portera le même que fbksl-nl g.indentation = 1 # compteur d'indentation attaché à gbksl-nl g.trace = True # booléen pour activer ou désactiver la tracebksl-nl g.tracepy-undpile = Falsebksl-nl g.pile = []bksl-nl DICOpy-undTRACE[f.py-undpy-undnamepy-undpy-und] = gbksl-nl return DICOpy-undTRACE[f.py-undpy-undnamepy-undpy-und]bksl-nlbksl-nlbksl-nldef desactiverpy-undtrace(fonction):bksl-nl if fonction.py-undpy-undnamepy-undpy-und in DICOpy-undTRACE:bksl-nl del DICOpy-undTRACE[fonction.py-undpy-undnamepy-undpy-und]bksl-nl fonction.trace = Falsebksl-nl bksl-nldef activerpy-undtracepy-undpile(fonction):bksl-nl if fonction.py-undpy-undnamepy-undpy-und in DICOpy-undTRACE:bksl-nl fonction.tracepy-undpile = Truebksl-nl bksl-nl bksl-nldef desactiverpy-undtracepy-undpile(fonction):bksl-nl if fonction.py-undpy-undnamepy-undpy-und in DICOpy-undTRACE:bksl-nl fonction.tracepy-undpile = Falsebksl-nl#--- HDR ---#bksl-nlimport sysbksl-nlbksl-nldef sommepy-undrec(n):bksl-nl """bksl-nl Renvoie la somme des entiers successifs de 1 à n :bksl-nl 1 + 2 + 3 + ... + nbksl-nl Fonction récursivebksl-nl Parametres:bksl-nl n (py-undintpy-und): entier naturelbksl-nl """bksl-nl # à compléterbksl-nl bksl-nldef sommepy-unditer(n):bksl-nl """bksl-nl Renvoie la somme des entiers successifs de 1 à n :bksl-nl 1 + 2 + 3 + ... + nbksl-nl Fonction itérative (avec boucle)bksl-nl Parametres:bksl-nl n (py-undintpy-und): entier naturelbksl-nl """bksl-nl # à compléterbksl-nl bksl-nlbksl-nldef test(somme):bksl-nl for n in range(1, 21):bksl-nl assert somme(n) == n py-str (n + 1) / 2bksl-nl print("Tests réussis")bksl-nl bksl-nl# Décommentez pour la question 1bksl-nl#test(sommepy-undrec)bksl-nl#test(sommepy-unditer)bksl-nlbksl-nl# Décommentez pour la question 2bksl-nl#sommepy-undrec = trace(sommepy-undrec)bksl-nl#activerpy-undtracepy-undpile(sommepy-undrec)bksl-nl bksl-nlbksl-nl bksl-nlbksl-nl

    🐍 Script Python
    def somme_rec(n):
    """
    Renvoie la somme des entiers successifs de 1 à n :
    1 + 2 + 3 + ... + n
    Fonction récursive
    Parametres:
        n (_int_): entier naturel
    """
    if n == 1:
        return 1
    return n + somme_rec(n - 1)
    
def somme_iter(n):
    """
    Renvoie la somme des entiers successifs de 1 à n :
    1 + 2 + 3 + ... + n
    Fonction itérative (avec boucle)
    Parametres:
        n (_int_): entier naturel
    """
    s = 0
    for k in range(1, n + 1):
        s = s + k
    return s
    

def test(somme):
    for n in range(1, 21):
        assert somme(n) == n * (n + 1) / 2
    print("Tests réussis")

  2. Cliquez sur le bouton ci-dessous pour exécuter les fonctions somme_iter et somme_rec sur la plage d'entiers compris entre 980 et 1000 dans Capytale. 1

    💻 Test sur Capytale

    Que remarquez-vous ?

    Stack Overflow

    On obtient le message d'erreur suivant qui nous indique que la profondeur maximale d'appels récursifs a été atteinte.

    🐍 Script Python
    >>> for n in range(980, 1001):
        print(n, somme_iter(n), somme_rec(n))

980 480690 480690
981 481671 481671
982 482653 482653
983 483636 483636
984 484620 484620
985 485605 485605
986 486591 486591
987 487578 487578
988 488566 488566

Traceback (most recent call last):
File "<input>", line 28, in <module>
File "<input>", line 12, in somme_rec
File "<input>", line 12, in somme_rec
File "<input>", line 12, in somme_rec
[Previous line repeated 985 more times]
File "<input>", line 9, in somme_rec
RecursionError: maximum recursion depth exceeded in comparison

Point de cours 5

Lorsqu'une fonction est appelée, un contexte est créé qui va contenir les variables locales de cette fonction.

Si une fonction B est appelée au cours de l'exécution de la fonction A, alors l'exécution de la fonction A est interrompue et son contexte est sauvegardé au sommet d'une pile. Il sera restauré dès la fin de l'appel de la fonction B et l'exécution de A pourra reprendre dans son contexte. Si on une fonction récursive, les fonctions A et B sont les mêmes et donc B peut encore s'appeler elle même, jusqu'au cas de base ... Au cours de la phase de descente, les contextes s'empilent, avec toujours le contexte du dernier appel au sommet. Dans la phase de remontée, les contextes sont dépilés et restaurés pour la fin de l'exécution de chaque appel de fonction, jusqu'à ce que la pile soit vide.

Les contextes des appels récursifs sont sauvegardés dans une pile d'appels. On donne une trace de la pile d'appels lors de l'évaluation de somme_rec(4).

Exemple de pile d'appels
🐍 Script Python
Appel de somme_rec(4) => descente 

État de la pile : 

|Contexte de somme_rec(4,)|
|-------------------------|




Appel de somme_rec(3) => descente 

État de la pile : 

|Contexte de somme_rec(3,)|
|-------------------------|
|Contexte de somme_rec(4,)|
|-------------------------|




Appel de somme_rec(2) => descente 

État de la pile : 

|Contexte de somme_rec(2,)|
|-------------------------|
|Contexte de somme_rec(3,)|
|-------------------------|
|Contexte de somme_rec(4,)|
|-------------------------|




Appel de somme_rec(1) => descente 

État de la pile : 

|Contexte de somme_rec(1,)|
|-------------------------|
|Contexte de somme_rec(2,)|
|-------------------------|
|Contexte de somme_rec(3,)|
|-------------------------|
|Contexte de somme_rec(4,)|
|-------------------------|




Fin de somme_rec(1) <=  remontée 

État de la pile : 

|Contexte de somme_rec(1,)|
|-------------------------|
|Contexte de somme_rec(2,)|
|-------------------------|
|Contexte de somme_rec(3,)|
|-------------------------|
|Contexte de somme_rec(4,)|
|-------------------------|



Fin de somme_rec(2) <=  remontée 

État de la pile : 

|Contexte de somme_rec(2,)|
|-------------------------|
|Contexte de somme_rec(3,)|
|-------------------------|
|Contexte de somme_rec(4,)|
|-------------------------|



Fin de somme_rec(3) <=  remontée 

État de la pile : 

|Contexte de somme_rec(3,)|
|-------------------------|
|Contexte de somme_rec(4,)|
|-------------------------|



Fin de somme_rec(4) <=  remontée 

État de la pile : 

|Contexte de somme_rec(4,)|
|-------------------------|

Chaque appel récursif consomme de la mémoire dans la pile d'appels. Une boucle réalisant le même nombre de répétitions n'a pas besoin d'enregistrer des états antérieurs pour y revenir. Une version récursive d'un algorithme est donc en général plus gourmande en mémoire que la version itérative, c'est pourquoi les langages de programmation comme Python prévoient un mécanisme de limitation de la taille de la pile d'appels. On peut la lire et la modifier avec des getter et setter.

🐍 Script Python
>>> import sys     
>>> sys.getrecursionlimit()  # lecture de la taille  pile d'appels
1000
>>> sys.setrecursionlimit(3000)  # modification de sa taille
>>> sys.getrecursionlimit()
3000

  1. Dans ce navigateur, Python est émulé avec Javascript et la limite de la taille de la pile est encore plus petite et ne permet pas des appels récursifs très profonds. La technologie utilisée est basée sur Pyodide, voir Pyodide-mkdocs. ↩