Algorithmes récursifs, fonctions récursives (Bac 🎯)⚓︎

Ce cours est mis à disposition selon les termes de la Licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.

Sources et crédits pour ce cours
Pour préparer ce cours, j'ai utilisé :
- le cours d'Olivier Lécluse
- le manuel NSI chez Ellipses de Balabonski, Conchon, Filliâtre, Nguyen
- le manuel NSI chez Hachette sous la direction de Michel Beaudouin Lafon
- la ressource Eduscol sur la récursivité
- le cour e-nsi sur la récursivité
- le cours de mon collègue Pierre Duclosson
🔖 Synthèse de ce qu'il faut retenir pour le bac
Algorithme d'Euclide⚓︎
Exemple 1
L'algorithme d'Euclide pour déterminer le Plus Grand Commun Diviseur de deux entiers naturels est l'un des plus anciens algorithmes connus.
Si on note PGCD(a, b) le PGCD des entiers naturels a et b et a % b le reste de la division euclidienne de a par b, alors la propriété fondamentale utilisée dans l'algorithme est que PGCD(a, b) = PGCD(b, a %b).
Déroulons l'algorithme dans le calcul de PGCD(100, 45).
Dans une première phase, dite de descente, on réduit chaque problème de calcul de PGCD à un problème de calcul de PGCD avec des entiers plus petits, jusqu'à ce qu'on atteigne un cas de base où la solution est immédiate car l'un des entiers divise l'autre.
- Problème 1 à résoudre
a = 100etb = 45eta % b = 10doncPGCD(100, 45) = PGCD(45, 10), on se ramène au calcul dePGCD(45, 10) - Problème 2 à résoudre
a = 45etb = 10eta % b = 5doncPGCD(45, 10) = PGCD(10, 5), on se ramène au calcul dePGCD(10, 5) - Problème 3 à résoudre
a = 10etb = 5eta % b = 0doncPGCD(10, 5) = PGCD(5, 0), on se ramène au calcul dePGCD(5, 0) - Problème 4 à résoudre
a = 5etb = 0doncadivisebdoncPGCD(5, 0) = 5c'est le cas de base
Ensuite, vient la phase de remontée de la réponse, du cas de base vers le problème initial :
- Problème 4 résolu
PGCD(5, 0) = 5 - donc Problème 3 résolu car
PGCD(10, 5) = PGCD(5, 0)doncPGCD(10, 5) = 5 - donc Problème 2 résolu car
PGCD(45, 10) = PGCD(10, 5)doncPGCD(45, 10) = 5 - donc Problème 1 résolu car
PGCD(100, 45) = PGCD(45, 10)doncPGCD(100, 45) = 5
récursif versus itératif
On donne ci-dessous deux implémentations en Python du calcul de PGCD avec l'algorithme d'Euclide.
pgcd_iteratif est une implémentation itérative c'est-à-dire avec une boucle qui permet de répéter les réductions successives du problème.
pgcd_recursif est une implémentation récursive c'est-à-dire que la fonction s'appelle elle-même pour réduire le problème
à un problème similaire mais sur des entiers plus petits.
💡 Pour répéter un traitement on disposait déjà de la boucle (programme itératif), on introduit ici l'appel d'une fonction par elle-même (programme récursif).
Exécutez le script puis dans la console évaluez :
pgcd_iteratif(100, 45)pgcd_recursif(100, 45)pgcd_recursif = trace(pgcd_recursif)puis à nouveaupgcd_recursif(100, 45)pour afficher une trace 1 de l'éxécution depgcd_recursif(100, 45)
>>> pgcd_iteratif(100, 45)
>>> pgcd_recursif(100, 45)
5
>>> pgcd_recursif = trace(pgcd_recursif)
>>> pgcd_recursif(100, 45)
┌Appel de recursion_wrapper(100) => descente
| ┌Appel de recursion_wrapper(45) => descente
| | ┌Appel de recursion_wrapper(10) => descente
| | | ┌Appel de recursion_wrapper(5) => descente
| | | └Fin de recursion_wrapper(5) <= remontée
| | └Fin de recursion_wrapper(10) <= remontée
| └Fin de recursion_wrapper(45) <= remontée
└Fin de recursion_wrapper(100) <= remontée
5
Définition d'une fonction récursive⚓︎
Point de cours 1
Un algorithme récursif est un algorithme qui résout un problème en se ramenant à la résolution de un ou plusieurs sous-problèmes similaires mais plus petits jusqu'à la résolution d'un cas de base dont la réponse est directe.
On distingue deux parties dans un algorithme récursif :
- la réduction consiste à réduire la résolution du problème initial de taille \(n\) à celle de un ou plusieurs sous-problèmes de même type et de taille inférieure (\(n-1\) ou \(n/2\) etc ...) : l'algorithme s'appelle alors lui-même sur ces sous-problèmes : on parle d'appels récursifs.
- la résolution directe pour un cas de base
Un algorithme récursif est implémenté sous la forme d'une fonction récursive.
💡Une fonction récursive est une fonction qui s'appelle elle-même.
Le code d'une fonction récursive suit donc en général un schéma avec un if ... else :
def fonction_rec(n):
# n entier naturel pour simplifier
if n in cas_de_base: # cas de base
return solution_directe
else:
return fonction_rec(reduction(n)) #avec reduction(n) < n
Arbre d'appels⚓︎
Méthode 1 : trace d'une fonction récursive
On peut représenter l'évaluation d'une fonction récursive par un arbre d'appels. Par exemple pour une fonction récursive de calcul du PGCD de deux entiers, on peut représenter ainsi les appels récursifs dans l'évaluation de PGCD(100, 45) lors de la phase de descente qui se termine par un cas de base :
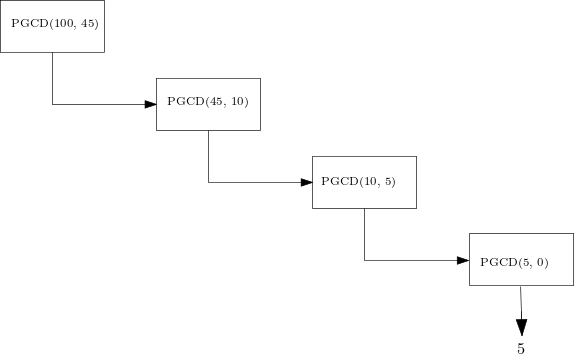
La phase de remontée depuis un cas de base s'effectue en remplaçant à rebours chaque appel récursif par sa valeur :
| Calculs à rebours | Arbre d'appels |
|---|---|
| PGCD(5,0) | 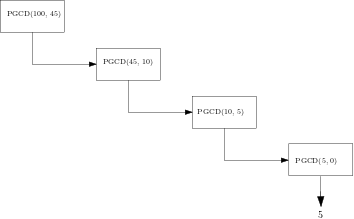 |
| PGCD(10,5) | 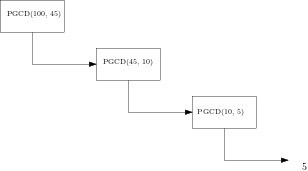 |
| PGCD(45, 10) | 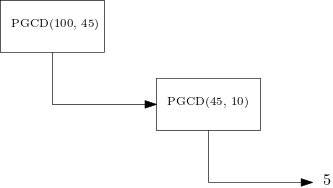 |
| PGCD(100,45) | 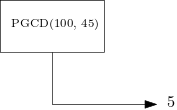 |
Maîtriser les compétences du programme⚓︎
Exercice 1
🎯 Analyser le fonctionnement d'un programme récursif
On donne trois fonction récursives en Python qui s'appliquent à des entiers naturels.
def f(n):
if n == 0:
return 1
else:
return n * f(n - 1)
def g(n):
return n * g(n - 1)
def h(n):
if n == 0:
return 1
else:
n * h(n - 1)
- Sans utiliser l'ordinateur, calculer les valeurs de
f(0),f(1),f(2),f(10). On complètera progressivement un arbre d'appels qu'on remontera à rebours depuis le cas de base pour calculer la valeur de l'appel initial. - Sans utiliser l'ordinateur, prévoir ce qui se passe si on évalue
f(-1),g(0),h(0),h(1)et enfinh(2).
-
Sans utiliser l'ordinateur, calculer les valeurs de
f(0),f(1),f(2),f(10).- 0 est le cas de base de la fonction récursive f donc par calcul direct f(0) vaut 1
-
1 n'est pas un cas de base, le calcul de f(1) se ramène par réduction à celui de f(1) = 1 * f(0). L'appel récursif se renvoie directement 1 car 0 est le cas de base donc f(1) = 1 * 1 = 1. Toujours par réductions successives, les appels récursifs s'imbriquent pour le calcul de f(2) :
📋 Textef(2) = 2 * f(1) = 2 * (1 * f(0)) = 2 * (1 * 1) = 2
Lors de l'évaluation de f(2), il faut bien comprendre que la séquence d'égalités est parcourue d'abord de gauche à droite (phase de descente) jusqu'à un cas de base, puis de droite à gauche (phase de remontée). * Pour f(10), les phases de descenter et remontée sont plus longues. On peut remarquer que le résultat est le produit des entiers successifs de 1 à 10, la factorielle de 10, notée 10!
📋 Textef(10) = 10 * f(9) = 10 * (9 * f(8)) = .... = 10 * (9 * (8 * ( ... * 1))) -
Sans utiliser l'ordinateur, prévoir ce qui se passe si on évalue
f(-1),g(0),h(0),h(1)et enfinh(2).- -1 n'est pas un cas de base donc par réduction le calcul de f(-1) se ramène au calcul de f(-2) qui lui-même se ramène au calcul de f(-3) puis de f(-4) etc ... Comme le cas de base est 0 et que chaque réduction décrémente le paramètre de 1, on n'atteindra jamais le cas de base, c'est une descente infinie.
Comme avec une boucle, une fonction récursive peut donc ne pas se terminer ! Ici cela se produit car le domaine de définition de la fonction Python est plus grand que celui de la fonction qu'on souhaite implémenter, il faudrait vérifier que le paramètre
npassé à la fonction est un entier naturel, par exemple avec une assertion. On parle de programmation défensive.
🐍 Script Pythondef f(n): assert isinstance(n, int) and n >= 0 # précondition if n == 0: return 1 else: return n * f(n - 1)- 0 n'est pas un cas de base pour la fonction récursive g donc par réduction le calcul de g(0) se ramène au calcul de g(-1) qui lui-même se ramène au calcul de g(-2) puis de f(-3) etc ... Nouvelle descente infinie. Ici, on n'atteindra jamais le cas de base, parce qu'il n'existe pas ! La fonction récursive ne se termine pas quel que soit son paramètre car le cas de base a été oublié !
- 0 est un cas de base pour la fonction récursive h et la valeur de h(0) est obtenue directement, c'est 1.
- 1 n'est pas un cas de base pour la fonction récursive h donc par réduction le calcul de h(1) se ramène au calcul de 1 * h(0) c'est-à-dire 1 * 1 puisque 0 est un cas de base. Notons que le calcul est effectué mais que h(1) ne renvoie rien car il n'y a pas de
returndans la branche de réduction. - 2 n'est pas un cas de base pour la fonction récursive h donc par réduction le calcul de h(2) se ramène au calcul de 2 * h(1). Mais la valeur renvoyée par h(1) est None puisqu'il n'y a pas de
returndans la branche de réduction. Le calcul2 * Nonen'a pas de sens car2etNonene sont pas de même type donc l'évaluation de h(2) provoque une erreur de type
- -1 n'est pas un cas de base donc par réduction le calcul de f(-1) se ramène au calcul de f(-2) qui lui-même se ramène au calcul de f(-3) puis de f(-4) etc ... Comme le cas de base est 0 et que chaque réduction décrémente le paramètre de 1, on n'atteindra jamais le cas de base, c'est une descente infinie.
Comme avec une boucle, une fonction récursive peut donc ne pas se terminer ! Ici cela se produit car le domaine de définition de la fonction Python est plus grand que celui de la fonction qu'on souhaite implémenter, il faudrait vérifier que le paramètre
Exercice 2
🎯 Écrire un programme récursif
On veut écrire une fonction récursive somme_carre qui prend en paramètre un entier naturel et qui renvoie la somme \(s(n)=0^{2}+1^2+2^2+3^2+...+n^2=\sum_{k=0}^{n}k^2\).
- Donner un ou plusieurs cas de base(s) dont la valeur peut être calculée directement.
- Soit \(n\) un entier naturel strictement positif, exprimer \(s(n)\) en fonction de \(s(n-1)\). Cette réduction s'appelle en mathématiques une relation de récurrence.
- Implémenter en Python la fonction récursive
somme_carredans l'IDE ci-dessous. Quelques tests unitaires sont fournis. - Calculer à la main
somme_carre(5)à l'aide d'un arbre d'appels. - Si ce n'est déjà fait, insérer une assertion au début de la fonction pour vérifier que le paramètre est un entier naturel et que le domaine de définition de la fonction Python correspond à celui qu'on souhaite.
- Donner une version itérative (avec une boucle) de cette fonction.
- \(s(0)=0\) est le cas de base, plus généralement \(s(n)=n\) pour \(0 \leqslant n \leqslant 1\).
- Pour tout entier \(n \geqslant 1\), on a réduit le problème de taille \(n\) au problème de taille \(n-1\) avec la relation de récurrence \(s(n)=s(n-1)+n^2\).
-
Implémentation en Python de la fonction récursive
somme_carre:🐍 Script Pythondef somme_carre(n): if n <= 1: return n return n ** 2 + somme_carre(n - 1) -
Calcul de
somme_carre(5)à la main avec un arbre d'appels :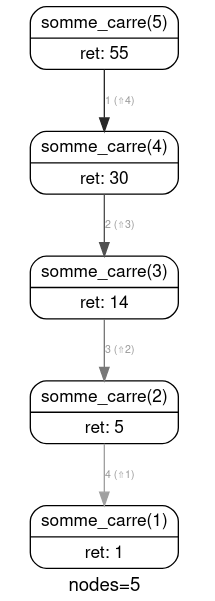
-
Avec programmation défensive :
🐍 Script Pythondef somme_carre(n): assert isinstance(n, int) and n >= 0 if n <= 1: return n return n ** 2 + somme_carre(n - 1) -
Version itérative :
🐍 Script Pythondef somme_carre_iter(n): assert isinstance(n, int) and n <= 1 s = 0 for k in range(1, n + 1): s = s + k ** 2 return s
-
la fonction
traceest cachée, elle prend en paramètre une fonction récursive et la transforme en une autre fonction de même nom pour qu'elle affiche la trace de l'exécution lorsqu'on appelle la fonction sur des paramètres. ↩