Problème du voyageur de commerce (Bac 🎯)⚓︎

Ce cours est mis à disposition selon les termes de la Licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.

Sources et crédits pour ce cours
Pour préparer ce cours, j'ai utilisé :
- le manuel NSI chez Ellipses de Balabonski, Conchon, Filliâtre, Nguyen dont est inspiré l'intégralité de cette partie sur le problème du voyageur de commerce
- le livre part 3 : greedy algorithms and dynamic programming de Tim Roughgarden
- page sur le problème du voyageur de commerce du site Interstices
🔖 Synthèse de ce qu'il faut retenir pour le bac
Un problème d'optimisation⚓︎
Problème du voyageur de commerce (Travelling Salesman Problem)
William Rowan Hamilton a posé pour la première fois ce problème, dès 1859. Sous sa forme la plus classique, son énoncé est le suivant :
Un voyageur de commerce doit visiter une et une seule fois un nombre fini de villes et revenir à son point d'origine. Trouvez l'ordre de visite des villes qui minimise la distance totale parcourue par le voyageur
Il s'agit d'un problème d'optimisation dont la spécification est la suivante :
- Entrée du problème : une liste de villes reliées deux à deux et le tableau des distances entre deux villes
- Sortie du problème : un cycle passant une fois et une seule par chaque ville avec retour à la ville de départ, telle que la distance totale, somme des distances séparant deux étapes successives, soit minimale.
On peut modéliser l'entrée du problème par un graphe pondéré dont les sommets sont les villes et les arêtes les liaisons entre les villes. Nous nous restreindrons au cas d'un graphe complet : chaque ville est reliée à toutes les autres.
Résoudre le problème du voyageur de commerce revient à trouver dans ce graphe un cycle passant par tous les sommets une unique fois (un tel cycle est dit hamiltonien) et qui soit de longueur minimale.
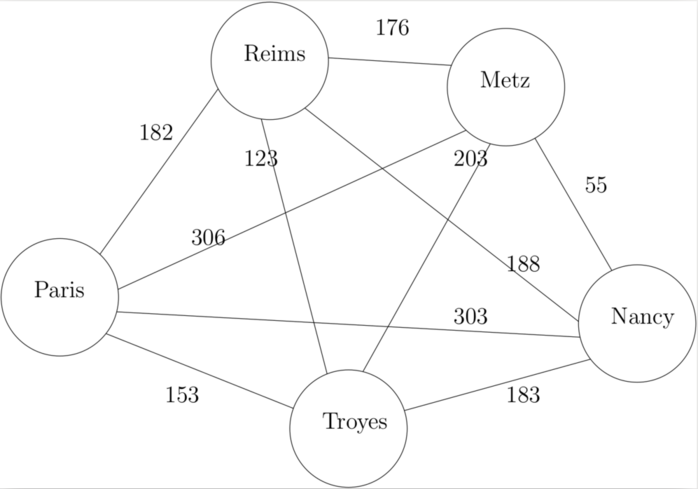
Exercice 1 : résolution par force brute
💻 Saisir ses réponses sur Capytale
Question 1
En explorant tous les circuits possibles, on peut déterminer un circuit de distance minimale.
Un tel algorithme est dit de recherche exhaustive ou de force brute.
On fournit ci-dessous une classe TSP1 pour créer une instance du problème à partir d'une liste de noms de villes et d'un tableau à deux dimensions des distances entre deux villes.
Chaque ville est repérée par son index dans l'attribut self.nom_ville et la distance entre les villes d'index 2 et 4 s'obtient avec self.distance[2][4] ou self.distance[4][2] puisque les distances entre deux villes sont symétriques.
-
Les index des villes dans
self.nom_villesont des entiers positifs compris entre 0 et un entiern(le nombre de villes - 1). Imaginez une urne remplie avec des jetons numérotées de 0 àn. Si on tire successivement et sans remise tous les jetons, on constitue une liste appelée permutation des entiers de 0 àn. La fonction récursivepermutationsprend en paramètre un entiernet renvoie une liste de toutes les permutations des entiers de 0 àn.- Quel est le nombre d'éléments dans la liste renvoyée par
permutations(1)?permutations(2)?permutations(3)? plus généralementpermutations(n)? - Compléter le code de la fonction
permutations - Comment créer un circuit hamiltonien à partir d'une des permutations renvoyées par la fonction
permutations?
- Quel est le nombre d'éléments dans la liste renvoyée par
-
Compléter le code de la méthode
meilleur_voyage_bruteforcede la classeTSP1: elle doit déterminer un circuit hamiltonien distance minimale sous forme de liste de noms de villes et renvoyer le couple (distance minimale, circuit).
Valeur de n |
Nombre de permutations des entiers de 0 à \(n\) |
|---|---|
| 1 | 2 |
| 2 | 6 |
| 3 | 24 |
| n | \((n+1)! = 1 \times 2 \times \ldots n \times (n+1)\) |
Les index des villes vont de \(0\) à un entier \(n\). Pour créer un circuit hamiltonien à partir d'une permuation renvoyée par permutations(n), il suffit d'ajouter à la fin le premier élément de la permutation pour boucler le circuit.
def permutations(n):
"""Renvoie toutes les permutations de la séquence d'entiers consécutifs [0, 1, 2, ..., n]"""
if n == 0:
return [[0]]
return [p[:i] + [n] + p[i:] for p in permutations(n - 1) for i in range(len(p) + 1)]
def test_permutations():
assert sorted(permutations(1)) == [[0, 1], [1, 0]]
assert sorted(permutations(2)) == [[0, 1, 2], [0, 2, 1], [1, 0, 2], [1, 2, 0], [2, 0, 1], [2, 1, 0]]
print("tests réussis pour permutations")
class TSP1:
"""Classe pour Travelling Salesman Problem"""
def __init__(self, v, d):
# liste de noms de villes
self.nom_ville = v
# nombre de villes
self.nb_villes = len(self.nom_ville)
# dictionnaire : nom de ville -> index dans self.nom_ville
self.index_ville = {self.nom_ville[k]: k for k in range(self.nb_villes)}
# tableau 2d des distances entre villes (repérées par leur index)
self.distance = d
def distance_circuit(self, circuit):
"""Distance totale parcourue dans le circuit hamiltonien circuit
qui est une liste d'indexs de villes dans self.nom_ville"""
d = 0
for k in range(len(circuit) - 1):
d = d + self.distance[circuit[k]][circuit[k + 1]]
return d
def meilleur_circuit_bruteforce(self):
"""Renvoie le couple (distance minimale, circuit minimal)
où circuit minimal est un circuit hamiltonien de distance minimale
"""
dmin = float('inf')
for p in permutations(self.nb_villes - 1):
circuit = p + [p[0]]
d = self.distance_circuit(circuit)
if d < dmin:
dmin = d
vmin = [self.nom_ville[v] for v in circuit]
return (dmin, vmin)
def test_circuit_brute_force():
nom_ville = ['Nancy', 'Metz', 'Paris', 'Reims', 'Troyes' ]
distance = [[0, 55, 303, 188, 183],
[55, 0, 306, 176, 203],
[303, 306, 0, 142, 153],
[188, 176, 142, 0, 123],
[183, 203, 153, 123, 0]]
tsp1 = TSP1(nom_ville, distance)
(dmin, vmin) = tsp1.meilleur_circuit_bruteforce()
vmin_nancy = vmin[vmin.index('Nancy'):-1] + vmin[:vmin.index('Nancy') + 1]
attendu = ['Nancy', 'Troyes', 'Paris', 'Reims', 'Metz', 'Nancy']
assert dmin == 709 and (vmin_nancy == attendu or vmin_nancy[::-1] == attendu)
print("tests réussis pour circuit_brute_force")
test_permutations()
test_circuit_brute_force()
Question 2
- Déterminer le nombre de circuits hamiltoniens distincts qui permettent de parcourir un graphe de \(n\) villes (cette fois numérotée de 1 à \(n\)) ?
- On considère que le nombre d'opérations qu'un programme peut exécuter en un temps raisonnable de quelques secondes est de l'ordre de \(10^{9}\). Donner un ordre de grandeur du nombre \(n\) de villes, que peut traiter le programme de recherche exhaustive d'un circuit hamiltonien de distance minimale ?
- Chaque circuit hamiltonien peut être associé de façon unique à l'une des \(n!\) permutations des entiers de \(1\) à \(n\). En regroupant les circuits dont l'ordre est inverse mais la distance totale identique, on peut considérer qu'il suffit de calculer le distances de \(\frac{n!}{2}\) circuits. De plus chaque circuit peut être commencé depuis n'importe quel sommet cela ne chabge pas la longueur donc cela nous donne \(\frac{n!}{2n}=\frac{(n-1)!}{2}\) circuits à considérer. L'algorithme force brute est donc de complexité \(O(n!)\) qui équivaut à \(O(n^{n}\sqrt{n}\text{e}^{-n})\) d'après la formule de Stirling.
- On a \(13! \approx 6,2 \times 10^{9}\) et \(12! \approx 4,8 \times 10^{8}\) donc un programme de recherche exhaustive ne peut traiter qu'un graphe d'entrée constituée d'une petite dizaine de villes.
Une heuristique gloutonne⚓︎
Heuristique gloutonne et algorithme glouton
On a vu qu'une recherche exhaustive peut résoudre de façon exacte le problème du voyageur de commerce mais ne peut pas être utilisée en pratique puisque par explosion combinatoire, la complexité de l'algorithme force brute est pire qu'exponentielle, en \(O(n!)\).
Si une solution exacte n'est pas accessible en un temps raisonnable, une bonne solution approchée peut être acceptable et même parfois s'avérer exacte ! On désigne par heuristique une méthode de résolution approchée.
Dans le problème du voyageur de commerce, un circuit solution est constitué d'une séquence de villes. On peut imaginer construire une solution approchée en insérant à chaque étape la ville qui fait le moins augmenter la longueur totale du circuit en cours. Une telle heuristique qui essaie d'approcher une solution globalement optimale par une succession de choix localement optimaux, s'appelle une heuristique gloutonne.
Un algorithme qui construit une solution avec une heuristique gloutonne est un algorithme glouton.
Si on a un problème d'optimisation dont une solution peut être construite itérativement mais pour lequel on ne connaît pas d'algorithme de résolution exacte efficace, alors un algorithme glouton peut être intéressant :
Caractéristiques d'un algorithme glouton
- Un algorithme glouton construit une solution par une succession de choix localement optimaux, en espérant obtenir une solution globalement optimale
- Un algorithme glouton est efficace, car il progresse directement vers une solution sans jamais remettre en question les choix précédents. Sa complexité est souvent facile à établir. Le travail pour effectuer chaque choix glouton est souvent effectué lors d'un prétraitement, par exemple avec un tri de l'entrée.
- Un algorithme glouton n'est pas toujours correct, et s'il l'est, la preuve peut être difficile.
Différences entre algorithmes Glouton et Diviser Pour Régner
| Thème | Algorithme glouton | Algorithme Diviser Pour Régner |
|---|---|---|
| Difficulté de conception | Facile | Difficile |
| Complexité | Facile à établir | Difficile à établir |
| Correction | Difficile à prouver | Facile à prouver (par récurrence) |
Problème difficile
Les problèmes que nous avons résolus par un algorithme (tri, recherche dans un tableau, parcours d'un arbre ...) peuvent être résolus en un nombre d'opérations inférieur à \(n^{p}\) (pour un certain \(p\)), on dit qu'ils appartiennent à la classe de complexité P pour polynomial.
Un problème de décision est une question, définie sur un ensemble d'entrées, dont la réponse sera Vrai ou Faux. Par exemple, étant donné l'ensemble des grilles incomplètes de Sudoku, un problème de décision consiste à déterminer pour une grille en entrée s'il existe une solution. Si on nous donne une grille complète solution, alors il est facile de vérifier en temps polynomial qu'elle est compatible. En revanche il est difficile de déterminer s'il existe une solution pour une grille incomplète et on ne connaît pas d'algorithme qui permet de le faire pour une grille quelconque en temps polynomial.
On dit que le problème de décision du Sudoku appartient à la classe de complexité NP : des problèmes difficiles pour lesquels il est facile de vérifier une solution. Mais ce n'est pas parce qu'on ne connaît pas d'algorithme polynomial pour répondre au problème de décision qu'il n'en existe pas.
Parmi les problèmes de la classe de complexité NP, certains sont NP-complet c'est-à-dire que la résolution de tout problème NP peut se ramener à celle d'un problème NP-complet en temps polynomial. Si on savait résoudre en temps polynomial un seul des problèmes NP-complet alors tous les problèmes NP seraient résolubles en temps polynomial et on aurait résolu la conjecture la classe NP est-elle égale à la classe P ? (on a bien sûr P \(\subset\) NP mais l'inclusion est-elle stricte ?).
Le problème de la classe de complexité NP associé au problème du voyageur de commerce est :
pour un graphe pondéré complet de \(n\) villes et un seuil fixé, existe-t-il un circuit hamiltonien de longueur totale inférieure à ce seuil ?
Si on nous donne une solution il est facile de vérifier que la somme des poids des arêtes est inférieure au seuil en parcourant le circuit. En revanche, on ne connaît pas d'algorithme en temps polynomial pour déterminer s'il existe une solution. Si on sait résoudre le problème de décision avec seuil alors on peut résoudre le problème du voyageur de commerce en faisant varier le seuil, par dichotomie par exemple.
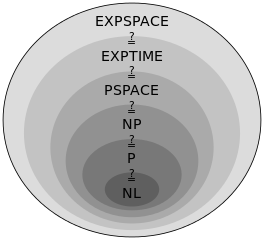
Source : Public Domain Wikipedia
Exercice 2 : résolution approchée du TSP par heuristique gloutonne
💻 Saisir ses réponses sur Capytale
On fournit ci-dessous une classe TSP2 similaire à TSP1 de l'exercice 1 avec un attribut supplémentaire self.visite qui est un tableau de booléens qui va permettre de tracer les villes déjà insérées dans le circuit lors de la construction d'un circuit hamiltonien avec une heuristique gloutonne.
self.visite(index_ville) vaudra True si la ville repérée par index_ville dans self.nom_ville est déjà dans la liste constituant le circuit et False sinon.
Question 1
Compléter la méthode plus_proche qui renvoie le couple (distance minimale, index de la ville la plus proche) pour une ville d'index passée en paramètre.
def plus_proche(self, va):
"""Renvoie le couple (distance minimale, index ville la plus proche)
pour une ville d'index va dans self.nom_ville
"""
dmin = float('inf')
for vb in range(self.nb_villes):
if vb != va and (not self.visite[vb]) and self.distance[va][vb] < dmin:
dmin = self.distance[va][vb]
vmin = vb
return (dmin, vmin)
Question 2
On peut appliquer une heuristique gloutonne simple pour construire de façon directe une solution approchée du problème du voyageur de commerce :
- on part d'une ville de départ quelconque
- à chaque étape on insère dans le circuit la ville pas encore visitée la plus proche de la dernière ville du circuit
- lorsque toutes les villes ont été visitées, on insère la ville de départ à la fin du circuit pour fermer la boucle
-
Compléter la méthode
meilleur_circuit_gloutonqui implémente cet algorithme glouton. -
La solution construite par cet algorithme glouton est-elle exacte ?
Cet algorithme glouton ne renvoie pas une solution exacte mais approchée, puisque le circuit glouton ['Nancy', 'Metz', 'Reims', 'Troyes', 'Paris', 'Nancy'] est de longueur 810 contre 709 pour le circuit minimal ['Nancy', 'Troyes', 'Paris', 'Reims', 'Metz', 'Nancy'] déterminé par recherche exhaustive.
def meilleur_circuit_glouton(self, nom_depart):
"""
Renvoie le couple (distance totale circuit, liste de noms
des villes d'un circuit hamiltonien construit par heuristique gloutonne)
"""
vd = self.index_ville[nom_depart]
derniere_etape = vd
circuit = [derniere_etape]
self.visite[derniere_etape] = True
dist_totale = 0
for _ in range(self.nb_villes - 1):
dist_etape, prochaine_etape = self.plus_proche(derniere_etape)
dist_totale = dist_totale + dist_etape
derniere_etape = prochaine_etape
circuit.append(derniere_etape)
self.visite[derniere_etape] = True
circuit.append(circuit[0])
dist_totale = dist_totale + self.distance[circuit[-2]][circuit[-1]]
return (dist_totale, [self.nom_ville[v] for v in circuit])